已知实数abc满足a+2b+c=1.a2+b2+c2=1.求证:-23≤c≤1．题目和参考答案——青夏教育精英家教网—

题目内容

已知实数abc满足a+2b+c=1，a²+b²+c²=1，求证：-

≤c≤1．

考点：二维形式的柯西不等式

专题：选作题,不等式

分析：对于“积和结构”或“平方和结构”，通常构造利用柯西不等式求解即可

解答： 证明：根据条件可得：a+2b=1-c，a²+b²=1-c²，
根据柯西不等式得：（a+2b）²≤（a²+b²）（1²+2²），
∴（1-c）²≤5（1-c²），
解之得：-

≤c≤1．

点评：柯西不等式的特点：一边是平方和的积，而另一边为积的和的平方，因此，当欲证不等式的一边视为“积和结构”或“平方和结构”，再结合不等式另一边的结构特点去尝试构造．

练习册系列答案

相关题目

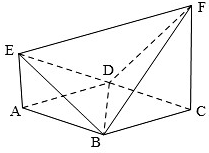如图，已知ABCD是边长为2的正方形，EA⊥平面ABCD，FC⊥平面ABCD，设EA=1，FC=2；
（1）证明：平面EAB⊥平面EAD；
（2）求四面体BDEF的体积；
（3）求点B到平面DEF的距离．

已知函数f（x）=x²+2ax+4．
（1）若函数f（x）满足f（1+x）=f（1-x），求函数在x∈[-2，2]的值域；
（2）在区间[-1，1]上，y=f（x）的图象恒在y=2x+1的图象上方，试确定实数a的范围．
（3）若方程f（x）=0在[-1，1]上有解，求实数a的取值范围．

某大学生创业团队淘宝项目每月要投入一定的营销费用，已知每投入营销费用k万元，每月销售收入大概增加-k²+5k+1万元．（利润=增加的销售收入-投入）
（Ⅰ）若该创业团队将本月的营销费用控制在3万元之内，则应投入多少营销费用才能使该项目本月利润最大．
（Ⅱ）现该创业团队本月准备投入3万元，分别用于营销费用和产品研发升级，经预测，产品研发升级费用每投入x万元增加的销售收入大概为-

x³+x²+3x万元，如何分配该笔资金，使该项目本月利润最大．

已知函数f（x）=2sin（ωx），其中常数ω＞0，令ω=2，将函数y=f（x）的图象向左平移个

单位，再向上平移1个单位，得到函数y=g（x）的图象，若函数y=g（z）在区间[m，m+10π]（-

＜m＜

5π

）上有20个零点：a₁，a₂，a₃，…，a₂₀，求a₁+a₂+a₃+…+a₂₀的值．

作为家长都希望自己的孩子能升上比较理想的高中，于是就催生了“名校热”，这样择校的结果就导致了学生在路上耽误的时间增加了．若某生由于种种原因，每天只能 6：15骑车从家出发到学校，途经5个路口，这5个路口将家到学校分成了6个路段，每个路段的骑车时间是10分钟（通过路口的时间忽略不计），假定他在每个路口遇见红灯的概率均为

，且该生只在遇到红灯或到达学校才停车．对每个路口遇见红灯情况统计如下：

红灯	1	2	3	4	5
等待时间（秒）	60	60	90	30	90

（1）设学校规定7：20后（含7：20）到校即为迟到，求这名学生迟到的概率；
（2）设X表示该学生上学途中遇到的红灯数，求P（X≥2）的值；
（3）设Y表示该学生第一次停车时已经通过路口数，求随机变量Y的分布列和数学期望．

设抛物线C：x²=2py（p＞0）的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F与l切于B点，且△ABF的面积为2．
（Ⅰ）求p的值及圆F的方程；
（Ⅱ）过B作直线与抛物线C交于M（x₁，y₁），N（x₂，y₂）两点，是否存在常数m，使

恒成立？若存在，求常数m的值；若不存在，请说明理由．

若3+2i（i为虚数单位）是关于x的方程x²+px+q=0（p，q∈R）的一个根，则q的值为

．

试题分类