题目内容
设变量x,y满足约束条件
,若目标函数z=ax+y取最大值时最优解不唯一,则a的值为( )
|
| A、-1 | B、0 | C、-1或1 | D、1 |
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,将z=ax+y化为y=-ax+z,z相当于直线y=-ax+z的纵截距,由几何意义可得.
解答:
解:由题意作出其平面区域,

将z=ax+y化为y=-ax+z,z相当于直线y=-ax+z的纵截距,
则由目标函数z=ax+y取最大值时最优解不唯一知,
y=-ax+z与y=4-x重合,
故a=1;
故选D.

将z=ax+y化为y=-ax+z,z相当于直线y=-ax+z的纵截距,
则由目标函数z=ax+y取最大值时最优解不唯一知,
y=-ax+z与y=4-x重合,
故a=1;
故选D.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个人以6米/秒的速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t内的路程为s=
t2米,那么,此人( )
| 1 |
| 2 |
| A、可在7秒内追上汽车 |
| B、可在9秒内追上汽车 |
| C、不能追上汽车,但其间最近距离为14米 |
| D、不能追上汽车,但其间最近距离为7米 |
已知a>b>c>0,则a2+
+
+
的最小值为( )
| 1 |
| bc |
| 1 |
| a(a-b) |
| 1 |
| b(a-c) |
| A、4 | B、6 | C、8 | D、10 |
已知实数x,y满足
则z=2x-y的最小值是( )
|
| A、5 | ||
B、
| ||
| C、-5 | ||
D、-
|
 如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )
如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )A、2
| ||
| B、4 | ||
C、4
| ||
| D、8 |
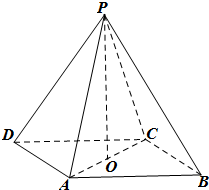 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.