题目内容
15.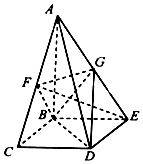 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.(Ⅰ)证明:EF⊥BD;
(Ⅱ)求点A到平面BFG的距离.
分析 (Ⅰ)取BC的中点M,连接MF,ME,证明BD⊥平面MEF,即可证明EF⊥BD;
(Ⅱ)利用VA-BFG=VG-ABF,求点A到平面BFG的距离.
解答 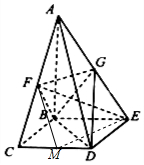 (Ⅰ)证明:取BC的中点M,连接MF,ME,
(Ⅰ)证明:取BC的中点M,连接MF,ME,
∵AB⊥平面BCDE,MF∥AB,
∴MF⊥平面BCDE,又BD?平面BCDE,∴MF⊥BD.
在Rt△MBE与Rt△BED中,∵$\frac{MB}{BE}$=$\frac{BE}{ED}$=$\frac{\sqrt{2}}{2}$,∴Rt△MBE∽Rt△BED.
∴∠BME=∠EBD,而∠BME+∠BEM=90°,于是∠BEM+∠EBD=90°,
∴ME⊥BD,
又∵MF∩ME=M,∴BD⊥平面MEF,
又∵EF?平面MEF,∴EF⊥BD.…(6分)
(Ⅱ)解:∵AB⊥平面BCDE,BE?平面BCDE,∴AB⊥BE,
∵四边形BCDE为矩形,∴BE⊥BC,
又∵AB∩BC=B,
∴BE⊥平面ABC,
∵G为AE的中点,
∴G到平面ABF的距离为$\frac{1}{2}$BE=$\frac{\sqrt{2}}{2}$,
S△ABF=$\frac{1}{2}$×2×1=1,
在△BFG中,FG=$\frac{1}{2}$CE=$\frac{\sqrt{6}}{2}$,BG=$\frac{1}{2}$AE=$\frac{\sqrt{6}}{2}$,BF=$\frac{1}{2}$AC=$\sqrt{2}$,
∴S△BFG=$\frac{\sqrt{2}}{2}$,
设A到平面BFG的距离为d,
∵VA-BFG=VG-ABF,
∴$\frac{1}{3}$•S△BFG•d=$\frac{1}{3}$•S△ABF•$\frac{\sqrt{2}}{2}$,
∴d=1,即A到平面BFG的距离为1.…(12分)
点评 本题考查线面垂直的判定与性质,考查等体积方法的运用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |

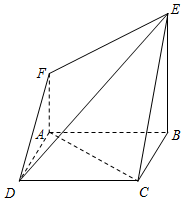 在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.
在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.