题目内容
10.侧棱与底面垂直的三棱柱A1B1C1-ABC的所有棱长均为2,则三棱锥B-AB1C1的体积为$\frac{2\sqrt{3}}{3}$.分析 先求出${S}_{△{A}_{1}{B}_{1}{C}_{1}}$,AA1=2,由此能求出三棱锥B-AB1C1的体积.
解答 解:∵侧棱与底面垂直的三棱柱A1B1C1-ABC的所有棱长均为2,
∴${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$,AA1=2,
∴三棱锥B-AB1C1的体积为:
V=$\frac{1}{3}×{S}_{△{A}_{1}{B}_{1}{C}_{1}}×A{A}_{1}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求不地,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
20.函数f(x)=log3(2x-1)的零点是( )
| A. | 1 | B. | 2 | C. | (1,0) | D. | (2,0) |
1.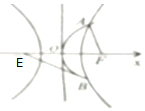 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
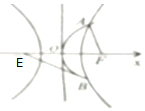 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )| A. | $4+\sqrt{7}$ | B. | $4-\sqrt{3}$ | C. | $4+\sqrt{3}$ | D. | $4-\sqrt{7}$ |
2. 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | 4 |
20.执行如图所示的程序框图,若输入的x值为1,则输出的k值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
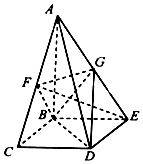 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.