题目内容
已知平行六面体ABCD-A1B1C1D1，AA1与平面A1B1C1D1垂直，且AD=AB，E为CC1中点，P在对角面BB1D1D所在平面内运动，若EP与AC成30°角，则点P轨迹为（ ）
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
考点：轨迹方程
专题：综合题,空间位置关系与距离
分析：确定对角面BB1D1D⊥底面ABCD，AC⊥对角面BB1D1D，取AA1的中点F，则EF∥AC，∵EP与AC成30°角，∴EP与EF成30°角，设EF与对角面BB1D1D的交点为O，则EO⊥对角面BB1D1D，考的点P轨迹为以EO为轴的一个圆锥的底面，EP是该圆锥的母线，且母线与底面成60°较，与轴成30°角，即可得出结论．
解答：
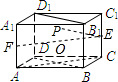解：∵平行六面体ABCD-A1B1C1D1，AA1与平面A1B1C1D1垂直，且AD=AB
∴平行六面体ABCD-A1B1C1D1是一个底面为菱形的直四棱柱，
∴对角面BB1D1D⊥底面ABCD，AC⊥对角面BB1D1D，
取AA1的中点F，则EF∥AC，∵EP与AC成30°角，∴EP与EF成30°角，
设EF与对角面BB1D1D的交点为O，则EO⊥对角面BB1D1D，
∴点P轨迹为以EO为轴的一个圆锥的底面，EP是该圆锥的母线，且母线与底面成60°较，与轴成30°角，
故选：A．
解：∵平行六面体ABCD-A1B1C1D1，AA1与平面A1B1C1D1垂直，且AD=AB∴平行六面体ABCD-A1B1C1D1是一个底面为菱形的直四棱柱，
∴对角面BB1D1D⊥底面ABCD，AC⊥对角面BB1D1D，
取AA1的中点F，则EF∥AC，∵EP与AC成30°角，∴EP与EF成30°角，
设EF与对角面BB1D1D的交点为O，则EO⊥对角面BB1D1D，
∴点P轨迹为以EO为轴的一个圆锥的底面，EP是该圆锥的母线，且母线与底面成60°较，与轴成30°角，
故选：A．
点评：本题考查轨迹方程，考察学生分析解决问题的能力，设EF与对角面BB1D1D的交点为O，确定EO⊥对角面BB1D1D是关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
函数y=
的定义域是（ ）
| 1 |
| x-2 |
| A、{x|x＜2} |
| B、{x|x＞2} |
| C、{x|x≠2} |
| D、{x|x≠0} |
已知函数f（x）=
，f2（x）=f（x），fn+1（x）=f（fn（x）），x∈N+，则f2015（x）=（ ）
| 1 |
| 1-x |
| A、x | ||
B、
| ||
C、
| ||
D、
|