题目内容
已知偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,且满足f(1-x)+f(1+x)=0,给出下列判断:
(1)f(5)=0;
(2)f(x)在[1,2]上是减函数;
(3)函数y=f(x)没有最小值;
(4)函数f(x)在x=0处取得最大值;
(5)f(x)的图象关于直线x=1对称.
其中正确的序号是 .
(1)f(5)=0;
(2)f(x)在[1,2]上是减函数;
(3)函数y=f(x)没有最小值;
(4)函数f(x)在x=0处取得最大值;
(5)f(x)的图象关于直线x=1对称.
其中正确的序号是
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:分别利用函数的奇偶性,单调性和周期性进行推理和判断,由f(1-x)+f(1+x)=0得到f(1+x)=-f(1-x)=-f(x-1),得到函数的周期为4.f(x+2)=-f(x),
解答:
解:
(1)由f(1-x)+f(1+x)=0
得到f(1+x)=-f(1-x)=-f(x-1),
设t=x-1.x=t+1,∴f(t+2)=-f(t),f(t+4)=f(t)
所以f(4+x)=f(x),所以函数的周期是4.
当x=0时,f(1)+f(1)=0,
所以f(1)=0,
因为f(5)=f(4+1)=f(1)=0,所以①正确.

(2)因为y=f(x)(x∈R)在区间[-1,0]上单调递增,周期为4,f(x+2)=-f(x),所以函数在区间[1,2]上单调递减,所以②正确.
(3)函数有最小值,也有最大值,且是相反数,故③错,
(4)∵偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,f(x+2)=-f(x),
∴函数f(x)在x=0处取得最大值;
(5)因为y=f(x)是偶函数,所以f(2+x)=-f(x),f(1)=0所以函数关于(1,0)对称.故⑤错误
因为偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,则在[0,1]上单调递减,且周期为4,所以y=f(x)在x=0处取得最大值,在x=-1时取得f(-1)=0.所以④正确,⑤错误.
故答案为:①②④
(1)由f(1-x)+f(1+x)=0
得到f(1+x)=-f(1-x)=-f(x-1),
设t=x-1.x=t+1,∴f(t+2)=-f(t),f(t+4)=f(t)
所以f(4+x)=f(x),所以函数的周期是4.
当x=0时,f(1)+f(1)=0,
所以f(1)=0,
因为f(5)=f(4+1)=f(1)=0,所以①正确.

(2)因为y=f(x)(x∈R)在区间[-1,0]上单调递增,周期为4,f(x+2)=-f(x),所以函数在区间[1,2]上单调递减,所以②正确.
(3)函数有最小值,也有最大值,且是相反数,故③错,
(4)∵偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,f(x+2)=-f(x),
∴函数f(x)在x=0处取得最大值;
(5)因为y=f(x)是偶函数,所以f(2+x)=-f(x),f(1)=0所以函数关于(1,0)对称.故⑤错误
因为偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,则在[0,1]上单调递减,且周期为4,所以y=f(x)在x=0处取得最大值,在x=-1时取得f(-1)=0.所以④正确,⑤错误.
故答案为:①②④
点评:本题主要考查函数的奇偶性,单调性和周期性的综合应用,要求熟练掌握相应的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知平行六面体ABCD-A1B1C1D1,AA1与平面A1B1C1D1垂直,且AD=AB,E为CC1中点,P在对角面BB1D1D所在平面内运动,若EP与AC成30°角,则点P轨迹为( )
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
若向量
满足|
|=2,且向量
与向量
-
的夹角等
,则|
|的最大值为( )
| a |
| a |
| b |
| b |
| a |
| π |
| 6 |
| b |
| A、2 | ||||
| B、4 | ||||
C、2
| ||||
D、
|
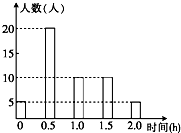 某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为