题目内容
求函数y=sin2x-4sinx+5的最值，并求取得最值时x的值．
考点：三角函数的最值
专题：函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析：首相把复合函数便形成标准式y=（sinx-2）2+1，然后根据函数sinx的值域确定整个复合函数的值域．
解答：
解：函数y=sin2x-4sinx+5=（sinx-2）2+1，
则：函数是以sinx为自变量的开口方向向上的抛物线．
①当sinx=1时，ymin=2，
即：当x=2kπ+
（k∈Z），函数取最小值，ymin=2，
②当sinx=-1时，ymax=10，
即：当x=2kπ-
（k∈Z），函数取最大值，ymax=10．
则：函数是以sinx为自变量的开口方向向上的抛物线．
①当sinx=1时，ymin=2，
即：当x=2kπ+
| π |
| 2 |
②当sinx=-1时，ymax=10，
即：当x=2kπ-
| π |
| 2 |
点评：本题考查的知识要点：复合函数的恒等变换，函数的最值问题的应用，属于基础题型．
练习册系列答案
相关题目
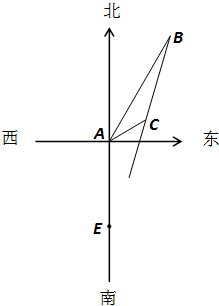在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40