题目内容
已知数列{an}的前n项和Sn满足SnS1=Sn+1（n∈N*），且a1=2，那么a7=（ ）
| A、128 | B、16 | C、32 | D、64 |
考点：数列的概念及简单表示法,数列递推式
专题：等差数列与等比数列
分析：利用等比数列的通项公式、递推式的意义即可得出．
解答：
解：∵数列{an}的前n项和Sn满足SnS1=Sn+1（n∈N*），a1=2，
∴Sn+1=2Sn，
∴Sn=2×2n-1=2n．
∴当n≥2时，an=Sn-Sn-1=2n-2n-1=2n-1．
∴a7=26=64．
故选：D．
∴Sn+1=2Sn，
∴Sn=2×2n-1=2n．
∴当n≥2时，an=Sn-Sn-1=2n-2n-1=2n-1．
∴a7=26=64．
故选：D．
点评：本题考查了等比数列的通项公式、递推式的意义，属于基础题．
练习册系列答案
相关题目
函数y=x2+bx+c（x∈[0，∞））是单调函数的充要条件是（ ）
| A、b≥0 | B、b＞0 |
| C、b＜0 | D、b≤0 |
计算
dx的值是（ ）
| ∫ | e 1 |
| 1 |
| x |
| A、0 | B、-1 | C、2 | D、1 |
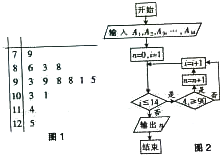如图是某高三学生14次数学考试成绩的茎叶图（图1），现在将该14个数据依次记为A1，A2，…，A14，并输入如图2所示的一个算法流程图，那么该算法流程图运行结束时输出n的值是（ ）| A、10 | B、9 | C、8 | D、7 |
