如果函数f=f=2.则$\frac{f}{f}+-+\frac{fA．1006B．2010C．2016D．4032 题目和参考答案——青夏教育精英家教网——

题目内容

18．如果函数f（x）对任意a，b满足f（a+b）=f（a）•f（b），且f（1）=2，则$\frac{f（2）}{f（1）}+\frac{f（4）}{f（3）}+\frac{f（6）}{f（5）}+…+\frac{f（2016）}{f（2015）}$=（　　）

A．

1006

B．

2010

C．

2016

D．

4032

分析令b=1，得f（a+1）=f（a）•f（1）=2f（a），得$\frac{f（a+1）}{f（a）}$=2，由此能求出结果．

解答解：∵函数f（x）满足：对任意实数a，b都有f（a+b）=f（a）f（b），且f（1）=2，
∴$\frac{f（2）}{f（1）}+\frac{f（4）}{f（3）}+\frac{f（6）}{f（5）}+…+\frac{f（2016）}{f（2015）}$=2+2+…+2=2
=2×1008=2016．
故选：C．

点评本题主要考查函数值的计算，根据条件寻找规律是解决本题的关键．

练习册系列答案

中学英才教程系列答案

教学大典系列答案

学考A加卷中考考点优化分类系列答案

发散思维新课堂系列答案

明日之星课时优化作业系列答案

同步首选全练全测系列答案

学效评估同步练习册系列答案

高中新课标同步用书全优课堂系列答案

实验探究报告册系列答案

金版学案高中同步辅导与检测系列答案

相关题目

8．设f（x）=e^x-e^-x，g（x）=e^x+e^-x．
（1）分别判断f（x），g（x）的奇偶性，并说明理由；
（2）求[f（x）]²-[g（x）]²的值．

9．平面几何中，若△ABC的内切圆半径为r，其三边长分别为a，b，c，则△ABC的面积$S=\frac{1}{2}（a+b+c）•r$．类比上述命题，若三棱锥的内切球半径为R，其四个面的面积分别为S₁，S₂，S₃，S₄，猜想三棱锥体积V的一个公式．若三棱锥P-ABC的体积V=$\frac{{2\sqrt{2}}}{3}$，其四个面的面积均为$\sqrt{3}$，根据所猜想的公式计算该三棱锥P-ABC的内切球半径R为（　　）

$\frac{{\sqrt{6}}}{6}$

$\frac{{\sqrt{6}}}{3}$

$\frac{{\sqrt{6}}}{12}$

$\frac{{\sqrt{6}}}{4}$

6．已知函数f（x）=x³+ax．
（Ⅰ）若f（x）在x=1处的切线平行于x轴，求a的值和f（x）的极值；
（Ⅱ）若过点A（1，0）可作曲线y=f（x）的三条切线，求a的取值范围．

13．给出下列命题：
①存在实数x，使得sinx+cosx=$\frac{3}{2}$；
②函数y=2sin（2x+$\frac{π}{3}$）的图象关于点（$\frac{π}{12}$，0）对称；
③若函数f（x）=ksinx+cosx的图象关于点（$\frac{π}{4}$，0）对称，则k=-1；
④在平行四边形ABCD中，若|$\overrightarrow{BC}$+$\overrightarrow{BA}$|=|$\overrightarrow{BC}$+$\overrightarrow{AB}$|，则四边形ABCD的形状一定是矩形．
则其中正确的序号是③④（将正确的判断的序号都填上）

3．幂函数的图象过点$（2，\sqrt{2}）$，则该幂函数的解析式为（　　）

$y={x^{\frac{1}{2}}}$

10．已知抛物线C：y²=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若$\overrightarrow{PF}$=3$\overrightarrow{QF}$，则|QF|=$\frac{8}{3}$．

7．设区域Ω={（x，y）|0≤x≤2，0≤y≤2}，区域A={（x，y）|xy≤1，（x，y）∈Ω}，在区域Ω中随机取一个点，则该点在A中的概率（　　）

$\frac{1+2ln2}{4}$

$\frac{1+2ln2}{8}$

$\frac{2ln2}{4}$

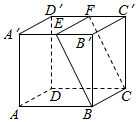如图，在正方体中，E，F是棱A′B′与D′C′的中点，求面EBCF与面ABCD所成二面角的正切值．（取锐角）