题目内容
7.设区域Ω={(x,y)|0≤x≤2,0≤y≤2},区域A={(x,y)|xy≤1,(x,y)∈Ω},在区域Ω中随机取一个点,则该点在A中的概率( )| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{1+2ln2}{8}$ | C. | $\frac{2ln2}{4}$ | D. | $\frac{1}{2}$ |
分析 由题意画出图形,求出正方形面积,再由定积分求出阴影部分的面积,代入几何概型概率计算公式得答案.
解答 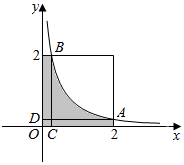 解:如图,
解:如图,
区域Ω={(x,y)|0≤x≤2,0≤y≤2}的面积为S=2×2=4,
区域A={(x,y)|xy≤1,(x,y)∈Ω}的面积S′=$\frac{1}{2}×2$+${∫}_{\frac{1}{2}}^{2}\frac{1}{x}dx=lnx{|}_{\frac{1}{2}}^{2}$=$1+ln2-ln\frac{1}{2}=1+2ln2$.
∴由几何概型概率计算公式可得:该点在A中的概率P=$\frac{1+2ln2}{4}$.
故选:A.
点评 本题考查几何概型,训练了利用定积分求曲边梯形的面积,是基础的计算题.

练习册系列答案
相关题目
17.根据$\sqrt{11-2}=3,\sqrt{1111-22}=33,\sqrt{111111-222}=333…$,猜得$\sqrt{\underbrace{11…1}_{2n个1}-\underbrace{22…2}_{n个2}}({n∈{N^+}})$的值是( )
| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{n+1个}$ | C. | $\underbrace{33…3}_{2n个}$ | D. | $\underbrace{33…3}_{2n-1个}$ |
18.如果函数f(x)对任意a,b满足f(a+b)=f(a)•f(b),且f(1)=2,则$\frac{f(2)}{f(1)}+\frac{f(4)}{f(3)}+\frac{f(6)}{f(5)}+…+\frac{f(2016)}{f(2015)}$=( )
| A. | 1006 | B. | 2010 | C. | 2016 | D. | 4032 |
12. 如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )
 如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )| A. | 14+6$\sqrt{5}$ | B. | 28+6$\sqrt{5}$ | C. | 28+12$\sqrt{5}$ | D. | 36+12$\sqrt{5}$ |
16.若函改数y=x3-ax2-x+6在区间(0,1)内单调递减.则实数a的取值范围为( )
| A. | a≥1 | B. | -1<a<0 | C. | a<0 | D. | 0<a<1 |