题目内容
解不等式:23x-2x<2(2x-2-x).
考点:指、对数不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:令2x=t(t>0),则23x-2x<2(2x-2-x)即为t3-t<2(t-
),化简整理即得1<t2<2,再由指数函数的单调性,即可解得.
| 1 |
| t |
解答:
解:令2x=t(t>0),
则23x-2x<2(2x-2-x)即为t3-t<2(t-
),
即有(t2-1)
<0,
即为1<t2<2,即有1<22x<2,
则0<2x<1,即为0<x<
,
故不等式的解集为(0,
).
则23x-2x<2(2x-2-x)即为t3-t<2(t-
| 1 |
| t |
即有(t2-1)
| t2-2 |
| t |
即为1<t2<2,即有1<22x<2,
则0<2x<1,即为0<x<
| 1 |
| 2 |
故不等式的解集为(0,
| 1 |
| 2 |
点评:本题考查指数不等式的解法,注意运用换元法,考查指数函数的单调性及运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
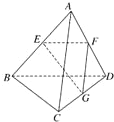 如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求:
如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求: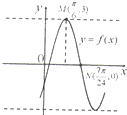 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<