题目内容
如图，在边长为2的正三角形ABC中，点P满足| CP |
| PB |
| AP |
| CB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的三角形法则、数量积运算性质即可得出．
解答：
解：∵点P满足
=2
，
∴
=
．
∴
•
=(
+
)•(-
)
=(-
+
)•(-
)
=
•
-
2
=2×2cos60°-
×22
=
．
故答案为：
．
| CP |
| PB |
∴
| BP |
| 1 |
| 3 |
| BC |
∴
| AP |
| CB |
| AB |
| BP |
| BC |
=(-
| BA |
| 1 |
| 3 |
| BC |
| BC |
=
| BA |
| BC |
| 1 |
| 3 |
| BC |
=2×2cos60°-
| 1 |
| 3 |
=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查了向量的三角形法则、数量积运算性质、等边三角形的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目
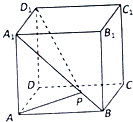如图所示，在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值，则此最小值为（ ）| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
方程ln（x+1）-
=0，（x＞0）的根存在的大致区间是（ ）
| 2 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，e） |
| D、（3，4） |
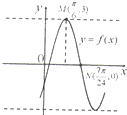如图，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜