题目内容
设θ为第二象限角,若sinθ+cosθ=
,则tan(θ+
)= .
| 1 |
| 5 |
| π |
| 4 |
考点:同角三角函数基本关系的运用,两角和与差的正切函数
专题:三角函数的求值
分析:已知等式两边平方,利用同角三角函数间基本关系化简求出sinθcosθ的值,原式利用两角和与差的正切函数公式化简,再利用同角三角函数间的基本关系变形,将各自得值代入计算即可求出值.
解答:
解:已知等式两边平方得:(sinθ+cosθ)2=1+2sinθcosθ=
,即sinθcosθ=-
,
∴(sinθ-cosθ)2=1-2sinθcosθ=
,
∵θ为第二象限角,
∴sinθ>0,cosθ<0,即cosθ-sinθ<0,
∴cosθ-sinθ=-
,
则tan(θ+
)=
=
=
=
=-
.
故答案为:-
| 1 |
| 25 |
| 12 |
| 25 |
∴(sinθ-cosθ)2=1-2sinθcosθ=
| 49 |
| 25 |
∵θ为第二象限角,
∴sinθ>0,cosθ<0,即cosθ-sinθ<0,
∴cosθ-sinθ=-
| 7 |
| 5 |
则tan(θ+
| π |
| 4 |
| tanθ+1 |
| 1-tanθ |
| ||
1-
|
| sinθ+cosθ |
| cosθ-sinθ |
| ||
-
|
| 1 |
| 7 |
故答案为:-
| 1 |
| 7 |
点评:此题考查了同角三角函数基本关系的运用,以及两角和与差的正切函数公式,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设x,y满足
(a>1),若函数z=x+y取得最大值4,则实数a=( )
|
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
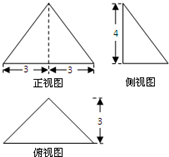 如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为( )
如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|