题目内容
1.已知${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3,则a+a-1=7,a2+a-2=47.分析 把${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3两边平方,求出a+a-1的值,同理求出a2+a-2的值.
解答 解:∵${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3,
∴${{(a}^{\frac{1}{2}}{+a}^{-\frac{1}{2}})}^{2}$=a+2+a-1=9,
∴a+a-1=7;
∴(a+a-1)2=a2+2+a-2=49,
∴a2+a-2=47.
故答案为:7,47.
点评 本题考查了完全平方公式的应用问题,也考查了幂的运算法则问题,是基础题目.

练习册系列答案
相关题目
16.若实数x,y满足$\sqrt{{x}^{2}+(y-13)^{2}}$-$\sqrt{{x}^{2}+(y+13)^{2}}$=10,则动点P(x,y)的轨迹方程是( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x>0) | B. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x<0) | ||
| C. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y>0) | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y<0) |
3.△ABC的三边长度分别是2,3,x,由所有满足该条件的x构成集合M,现从集合M中任取一x值,所得△ABC恰好是钝角三角形的概率为( )
| A. | $\frac{{4-\sqrt{13}+\sqrt{5}}}{4}$ | B. | $\frac{{5-\sqrt{13}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{5}-1}}{4}$ |
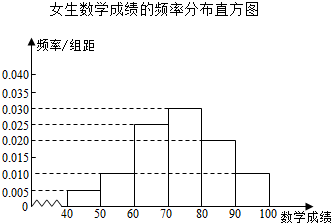
4.某校为了解高一学生的数学水平,随机抽取了高一男,女生各40人参加数学等级考试,得到男生数学成绩的频数分布表和女生数学成绩的频率分布直方图如下:
男生数学成绩的频数分布表
(Ⅰ)画出男生数学成绩的频率分布直方图,并比较该校高一男,女生数学成绩的方差大小;(只需写出结论)
(Ⅱ)根据女生数学成绩的频率分布直方图,估计该校高一女生的数学平均成绩;
(Ⅲ)依据学生的数学成绩,将学生的数学水平划分为三个等级:
估计该校高一男,女生谁的“数学水平良好”的可能性大,并说明理由.
男生数学成绩的频数分布表
| 成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 16 | 10 | 4 |

(Ⅰ)画出男生数学成绩的频率分布直方图,并比较该校高一男,女生数学成绩的方差大小;(只需写出结论)
(Ⅱ)根据女生数学成绩的频率分布直方图,估计该校高一女生的数学平均成绩;
(Ⅲ)依据学生的数学成绩,将学生的数学水平划分为三个等级:
| 数学成绩 | 低于70分 | 70~90分 | 不低于90分 |
| 数学水平 | 一般 | 良好 | 优秀 |
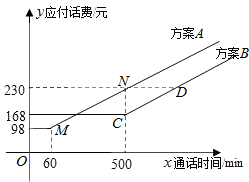 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230).
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230).