题目内容
已知f(x)=2+log3x,x∈[1,3],求y=[f(x)]2+f(x)的最大值及相应的x的值.
考点:对数函数图象与性质的综合应用
专题:计算题
分析:根据f(x)的定义域为[1,3]先求出y的定义域为[0,1],然后即可确定y=[f(x)]2+f(x)的最大值及相应的x的值.
解答:
解:由f(x)的定义域为[1,3]可得y的定义域为[0,1],
又y=(2+log3x)2+(2+log3x)=(log3x+3)(log3x+2),
∵1≤x≤3,∴0≤log3x≤1.
∴当x=3时,g(x)有最大值12.
又y=(2+log3x)2+(2+log3x)=(log3x+3)(log3x+2),
∵1≤x≤3,∴0≤log3x≤1.
∴当x=3时,g(x)有最大值12.
点评:本题主要考察了对数函数图象与性质的综合应用,其中根据f(x)的定义域先求出y的定义域是正确解题的关键步骤,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若向量
=(1,λ,1),
=(2,-1,1)且
与
的夹角的余弦值为
,则λ等于( )
| a |
| b |
| a |
| b |
| 1 |
| 6 |
| A、2 | ||
| B、-2 | ||
C、-2或
| ||
D、2或
|
已知函数f(x)=
-log2x,在下列区间中,包含f(x)零点的区间是( )
| 6 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,4) |
| D、(4,+∞) |
方程x2+(m-3)x+m=0有两个正实数根,则m的取值范围是( )
| A、0≤m<1 |
| B、0<m<1 |
| C、0<m≤1 |
| D、0≤m≤1 |
数列1,3,6,10,…的一个通项公式是( )
| A、an=n2-n+1 | ||
B、an=
| ||
C、an=
| ||
| D、an=n2+1 |
若a>0且a≠1,那么函数y=ax与y=logax的图象关于( )
| A、原点对称 | B、直线y=x对称 |
| C、x轴对称 | D、y轴对称 |
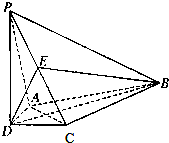 如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.
如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.