题目内容
下列各式中错误的是( )
| A、30.9>30.8 | ||||
| B、log0.50.4>log0.50.5 | ||||
| C、0.65-0.1<0.650.1 | ||||
D、3 -
|
考点:对数值大小的比较
专题:函数的性质及应用
分析:A.考察指数函数y=3x在R上单调递增,即可判断出;
B.考察对数函数y=log0.5x在(0,+∞)上单调递减,即可判断出;
C.考察指数函数y=0.65x在R上单调递减,即可判断出;
D.考察幂函数y=x-
在在(0,+∞)上单调递减,即可判断出.
B.考察对数函数y=log0.5x在(0,+∞)上单调递减,即可判断出;
C.考察指数函数y=0.65x在R上单调递减,即可判断出;
D.考察幂函数y=x-
| 1 |
| 2 |
解答:
解:A.∵指数函数y=3x在R上单调递增,∴30.9>30.8,正确;
B.∵对数函数y=log0.5x在(0,+∞)上单调递减,∴log0.50.4>log0.50.5,正确;
C.∵指数函数y=0.65x在R上单调递减,∴0.65-0.1>0.650.1,因此错误;
D.考察幂函数y=x-
在在(0,+∞)上单调递减,∴3-
<2-
,正确.
故选:C.
B.∵对数函数y=log0.5x在(0,+∞)上单调递减,∴log0.50.4>log0.50.5,正确;
C.∵指数函数y=0.65x在R上单调递减,∴0.65-0.1>0.650.1,因此错误;
D.考察幂函数y=x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查了指数函数对数函数与幂函数的单调性,属于基础题.

练习册系列答案
相关题目
方程x2+(m-3)x+m=0有两个正实数根,则m的取值范围是( )
| A、0≤m<1 |
| B、0<m<1 |
| C、0<m≤1 |
| D、0≤m≤1 |
若a>0且a≠1,那么函数y=ax与y=logax的图象关于( )
| A、原点对称 | B、直线y=x对称 |
| C、x轴对称 | D、y轴对称 |
如图是把二进制数11111(2)化为十进制数的一个程序框图,则判断框内应填入的条件是( )


| A、i>4 | B、i≤4 |
| C、i>5 | D、i≤5 |
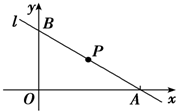 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△ABO的面积的最小值及此时直线l的方程.
已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△ABO的面积的最小值及此时直线l的方程.