题目内容

17．若直线ax+2y+6=0和直线x+a（a+1）y+a2-1=0垂直，则a=0或$-\frac{3}{2}$．

分析 由a（a+1）=0，解得a=0或-1．验证两条直线是否垂直．由a（a+1）≠0，由$-\frac{a}{2}×（-\frac{1}{a（a+1）}）=-1$，解得a即可得出．

解答 解：由a（a+1）=0，解得a=0或-1．
经过验证只有a=0时，两条直线相互垂直．
由a（a+1）≠0，由$-\frac{a}{2}×（-\frac{1}{a（a+1）}）=-1$，解得a=-$\frac{3}{2}$（验证分母不等于0）．
综上可得：a=-$\frac{3}{2}$或0．
故答案为：0或$-\frac{3}{2}$．

点评 本题考查了两条直线相互垂直的充要条件、分类讨论方法、方程的解法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
7．已知向量$\overrightarrow a$=（$\sqrt{3}$sin3x，-y），$\overrightarrow b$=（m，cos3x-m）（m∈R），且$\overrightarrow a$+$\overrightarrow b$=$\overrightarrow 0$．设y=f（x）．
（1）求f（x）的表达式，并求函数f（x）在[${\frac{π}{18}$，$\frac{π}{3}}$]上图象最低点M的坐标．
（2）在△ABC中，f（A）=-$\sqrt{3}$，且A＞$\frac{4}{9}$π，D为边BC上一点，AC=$\sqrt{3}$DC，BD=2DC，且AD=2$\sqrt{2}$，求线段DC的长．
8．已知集合A={log2x，4，8}，B={4，5}．若A∪B={1，4，5，8}，则实数x的值为2，A∩B={4}；令U=A∪B，则∁UA={5}．
5．已知函数f（x）=ex+ax，（a∈R），其图象与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2．
（1）证明：a＜-e；
（2）证明：$f'（{\frac{{{x_1}+{x_2}}}{2}}）＜0$；（其中f'（x）为f（x）的导函数）．
（3）设点C在函数f（x）的图象上，且△ABC为等边三角形，记$\sqrt{\frac{x_2}{x_1}}=t$，求$（t-1）（a+\sqrt{3}）$的值．
12．已知复数z=（2+i）m2-$\frac{6m}{1-i}$-2（1-i），当实数m取什么值时，复数z是 
（1）虚数，
（2）纯虚数．
2．已知椭圆C：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的上下焦点分别为F1，F2离心率为$\frac{1}{2}$，P为C上动点，且满足$\overrightarrow{{F}_{2}P}$=λ$\overrightarrow{PQ}$（λ＞0），|$\overrightarrow{PQ}$|=|$\overrightarrow{P{F}_{1}}$|，△QF1F2面积的最大值为4．
（Ⅰ）求Q点轨迹E的方程和椭圆C的方程；
（Ⅱ）直线y=kx+m（m＞0）与椭圆C相切且与曲线E交于M，N两点，求|MN|的取值范围．
9．设函数f（x）=x2+3x-2，则 $\lim_{△x→0}\frac{{f（{1+2△x}）-f（1）}}{△x}$=（　　）
A．5B．-5C．10D．-10
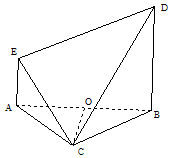6．如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，AE⊥AB，BC=BD=2AE=2，O为AB的中点．
（1）证明：CO⊥DE；
（2）求二面角C-DE-A的大小．
7．已知$\overrightarrow a=（{1，λ}），\overrightarrow b=（{2，1}）$，若向量$2\overrightarrow a+\overrightarrow b$与$\overrightarrow c=（{8，6}）$共线，则$\overrightarrow a$在$\overrightarrow b$方向上的投影为$\frac{3\sqrt{5}}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网