题目内容
13.已知某几何体的三视图如图所示,则此几何体的体积是( )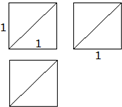
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 该几何体是由一个正方体切去两个小三棱锥后余下的几何体,如图所示.
解答  解:由已知中的三视图可得:
解:由已知中的三视图可得:
该几何体是由一个正方体切去两个小三棱锥后余下的几何体,如图所示:
该几何体的体积V=$1-2×\frac{1}{3}×\frac{1}{2}×{1}^{2}$=$\frac{2}{3}$.
故选:B.
点评 本题考查了正方体的三视图与体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知几何体的三视图如图所示,则该几何体的体积为( )
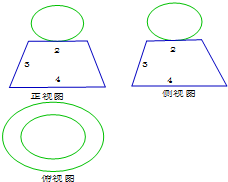

| A. | $\frac{π}{3}(4+14\sqrt{2})$ | B. | $\frac{{14\sqrt{2}π}}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{4π}{3}$ |
5.根据国家最新人口发展战略,一对夫妇可生育两个孩子,为了解人们对放开生育二胎政策的意向,某机构在A城市随机调查了100位30到40岁已婚人群,得到情况如表:
(Ⅰ)是否有95%以上的把握认为“生二胎与性别有关”,并说明理由(请参考所附的公式及相关数据);
(Ⅱ)从这60名男性中按对生育二胎政策的意向采取分层抽样,抽取6名男性,从这6名男性中随机选取两名,求选到的两名都愿意生育二胎的概率.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 意向 | 男 | 女 | 合计 |
| 生 | 40 | 20 | 60 |
| 不生 | 20 | 20 | 40 |
| 合计 | 60 | 40 | 100 |
(Ⅱ)从这60名男性中按对生育二胎政策的意向采取分层抽样,抽取6名男性,从这6名男性中随机选取两名,求选到的两名都愿意生育二胎的概率.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
5.已知等比数列{an}中,a1+a2+a3+a4+a5=31,a2+a3+a4+a5+a6=62,则通项an等于( )
| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
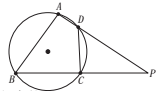 如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P.
如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P.