题目内容
已知甲、乙两地距丙的距离均为100km，且甲地在丙地的北偏东20°处，乙地在丙地的南偏东40°处，则甲乙两地的距离为（ ）
| A、100km | ||
| B、200km | ||
C、100
| ||
D、100
|
考点：解三角形的实际应用
专题：应用题,解三角形
分析：根据甲、乙两地距丙的距离均为100km，且甲地在丙地的北偏东20°处，乙地在丙地的南偏东40°处，利用余弦定理即可求出甲乙两地的距离．
解答：
解：由题意，如图所示OA=OB=100km，∠AOB=120°，
∴甲乙两地的距离为AB=
=100
km，
故选：D．
解：由题意，如图所示OA=OB=100km，∠AOB=120°，∴甲乙两地的距离为AB=
| 1002+1002-2×100×100×cos120° |
| 3 |
故选：D．
点评：本题考查解三角形的实际应用，考查余弦定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
如图给出的是计算
+
+
+…+
的值的一个程序框图，其中判断框中应填入的是（ ）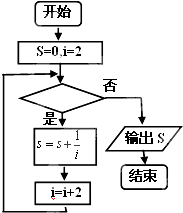
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
| A、i＞100 | B、i≤100 |
| C、i＞50 | D、i≤50 |
已知函数f（x）=
，其中a＞0，x∈（0，b]，则下列判断正确的是（ ）
| a+x2 |
| x |
A、当b＞
| ||||
B、当0＜b≤
| ||||
C、当0＜b≤
| ||||
D、当b＞0时，f（x）的最小值为2
|