题目内容
△ABC的内角A,B,C所对的边分别为a,b,c.
(1)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(2)在△ABC中,若S△ABC=
(b2+c2-a2),求角A的大小.
(1)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(2)在△ABC中,若S△ABC=
| 1 |
| 4 |
考点:余弦定理
专题:解三角形
分析:(1)由a,b,c成等差数列,利用等差数列的性质得到2b=a+c,利用正弦定理化简,整理即可得证;
(2)利用三角形面积公式列出关系式,代入已知等式求出tanA的值,即可确定出A的度数.
(2)利用三角形面积公式列出关系式,代入已知等式求出tanA的值,即可确定出A的度数.
解答:
(1)证明:∵a,b,c成等差数列,
∴2b=a+c,即2sinB=sinA+sinC,
∴sinA+sinC=2sin(A+C);
(2)解:∵S△ABC=
bcsinA=
(b2+c2-a2),
∴sinA=
,
又∵cosA=
,
∴sinA=cosA,即tanA=1,
∵0<A<π,
∴A=
.
∴2b=a+c,即2sinB=sinA+sinC,
∴sinA+sinC=2sin(A+C);
(2)解:∵S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
∴sinA=
| b2+c2-a2 |
| 2bc |
又∵cosA=
| b2+c2-a2 |
| 2bc |
∴sinA=cosA,即tanA=1,
∵0<A<π,
∴A=
| π |
| 4 |
点评:此题考查了余弦定理,正弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
函数y=kx+b与函数y=
在同一坐标系中的大致图象正确的是( )
| kb |
| x |
A、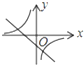 |
B、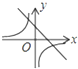 |
C、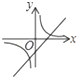 |
D、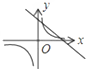 |
已知甲、乙两地距丙的距离均为100km,且甲地在丙地的北偏东20°处,乙地在丙地的南偏东40°处,则甲乙两地的距离为( )
| A、100km | ||
| B、200km | ||
C、100
| ||
D、100
|
函数f(x)=ax-1+2经过定点( )
| A、(2,2) |
| B、(2,3) |
| C、(1,2) |
| D、(1,3) |
函数y=ax-2-1(a>0且a≠1)的图象必经过点( )
| A、(0,1) |
| B、(1,1) |
| C、(2,0) |
| D、(2,2) |
在钝角△ABC中,“sinA=
”是“∠A=
”的( )
| ||
| 2 |
| 2π |
| 3 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
函数f(x)=x3+2x,则f(2)+f(-2)=( )
| A、0 | B、1 | C、2 | D、28 |