题目内容
函数y=loga（3x-1）恒过定点 ．
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：由对数定义知，函数y=logax图象过定点（1，0），故可令3x-1=1求此对数型函数图象过的定点．
解答：
解：由对数函数的定义，
令3x-1=1，此时y=0，
解得x=
，
故函数y=loga（3x-1）的图象恒过定点（
，0）
故答案为（
，0）．
令3x-1=1，此时y=0，
解得x=
| 2 |
| 3 |
故函数y=loga（3x-1）的图象恒过定点（
| 2 |
| 3 |
故答案为（
| 2 |
| 3 |
点评：本题考点是对数函数的单调性与特殊点，考查对数函数恒过定点的问题，由对数函数定义可直接得到真数为1时对数式的值一定为0，利用此规律即可求得函数图象恒过定点的坐标
练习册系列答案
相关题目
如图所示，网格纸上小正方形的边长为1cm，粗实线为某空间几何体的三视图，则该几何体的体积为（ ）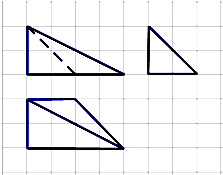
| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
设p：x∈R，q：2＜x＜3，则p是q成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知集合M={x|0≤x≤6}，P={y|0≤y≤3}，则下列对应关系中，不能看作从M到P的映射的是（ ）
| A、f：x→y=x | ||
B、f：x→y=
| ||
C、f：x→y=
| ||
D、f：x→y=
|