题目内容
已知函数f(x)=
+
-lnx-
,其中a∈R,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=
x.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间与极值.
| x |
| 4 |
| a |
| x |
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间与极值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)由曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=
x可得f′(1)=-2,可求出a的值;
(Ⅱ)根据(I)可得函数的解析式和导函数的解析式,分析导函数的符号,进而可得函数f(x)的单调区间与极值.
| 1 |
| 2 |
(Ⅱ)根据(I)可得函数的解析式和导函数的解析式,分析导函数的符号,进而可得函数f(x)的单调区间与极值.
解答:
解:(Ⅰ)∵f(x)=
+
-lnx-
,
∴f′(x)=
-
-
,
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=
x.
∴f′(1)=
-a-1=-2,
解得:a=
.
(Ⅱ)由(Ⅰ)知:f(x)=
+
-lnx-
,
f′(x)=
-
-
=
(x>0),
令f′(x)=0,
解得x=5,或x=-1(舍),
∵当x∈(0,5)时,f′(x)<0,当x∈(5,+∞)时,f′(x)>0,
故函数f(x)的单调递增区间为(5,+∞);
单调递减区间为(0,5);
当x=5时,函数取极小值-ln5.
| x |
| 4 |
| a |
| x |
| 3 |
| 2 |
∴f′(x)=
| 1 |
| 4 |
| a |
| x2 |
| 1 |
| x |
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=
| 1 |
| 2 |
∴f′(1)=
| 1 |
| 4 |
解得:a=
| 5 |
| 4 |
(Ⅱ)由(Ⅰ)知:f(x)=
| x |
| 4 |
| 5 |
| 4x |
| 3 |
| 2 |
f′(x)=
| 1 |
| 4 |
| 5 |
| 4x2 |
| 1 |
| x |
| x2-4x-5 |
| 4x2 |
令f′(x)=0,
解得x=5,或x=-1(舍),
∵当x∈(0,5)时,f′(x)<0,当x∈(5,+∞)时,f′(x)>0,
故函数f(x)的单调递增区间为(5,+∞);
单调递减区间为(0,5);
当x=5时,函数取极小值-ln5.
点评:本题考查的知识点是利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值,是导数的综合应用,难度中档.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知△ABC的内角A,B,C满足sin2A+sin(A-B+C)=sin(C-A-B)+
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
| 1 |
| 2 |
| A、bc(b+c)>8 | ||
B、ab(a+b)>16
| ||
| C、6≤abc≤12 | ||
| D、12≤abc≤24 |
数列{an}中,an+1=
,已知该数列既是等差数列又是等比数列,则该数列的前20项的和等于( )
| an2 |
| 2an-5 |
| A、100 |
| B、0或100 |
| C、100或-100 |
| D、0或-100 |
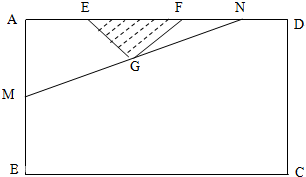 某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)
某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)