题目内容
4.在△ABC中,角A,B,C所对的边分别为a,b,c,已知$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}•\overrightarrow{BC}$,sinA=$\frac{3}{5}$(1)求sinC的值;
(2)设D为AC的中点,若BD的长为$\frac{\sqrt{153}}{2}$,求△ABC的面积.
分析 (1)在△ABC中,$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}•\overrightarrow{BC}$⇒bccosA=cacosB,即bcosA=acosB,利用正弦定理可得sin(A-B)=0,即A=B,再由sinA=$\frac{3}{5}$,求得cosA=$\frac{4}{5}$,于是可求sinC的值;
(2)D为AC的中点,BD的长为$\frac{\sqrt{153}}{2}$,则由$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)⇒a2+c2+$\frac{8}{5}$ac=153①;在△ABD中,利用余弦定理由|BD|2=|AB|2+|AD|2-2|AB|•|AD|cosA⇒c2+${(\frac{a}{2})}^{2}$-2c•$\frac{a}{2}$×$\frac{4}{5}$=$\frac{153}{4}$②
联立①②,可解得:a=5,c=8,从而可求得△ABC的面积.
解答 解:(1)在△ABC中,∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}•\overrightarrow{BC}$,
∴bccosA=cacosB,即bcosA=acosB,
由正弦定理得:sinBcosA=sinAcosB,即sin(A-B)=0,
∴A=B,即△ABC为等腰三角形.
又sinA=$\frac{3}{5}$,∴cosA=$\sqrt{1{-sin}^{2}A}$=$\frac{4}{5}$,
∴sinC=sin(π-A-B)=sin(π-2A)=sin2A=2sinAcosA=2×$\frac{3}{5}$×$\frac{4}{5}$=$\frac{24}{25}$;
(2)∵D为AC的中点,|BD|=$\frac{\sqrt{153}}{2}$,
∴$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$),
∴${\overrightarrow{BD}}^{2}$=$\frac{1}{4}$(${\overrightarrow{BA}}^{2}$+2$\overrightarrow{BA}$•$\overrightarrow{BC}$+${\overrightarrow{BC}}^{2}$),即$\frac{153}{4}$=$\frac{1}{4}$(c2+2accosB+a2),整理得:a2+c2+$\frac{8}{5}$ac=153①;
在△ABD中,由余弦定理得:|BD|2=|AB|2+|AD|2-2|AB|•|AD|cosA,即c2+${(\frac{a}{2})}^{2}$-2c•$\frac{a}{2}$×$\frac{4}{5}$=$\frac{153}{4}$②
联立①②,解得:a=5,c=8,
∴△ABC的面积S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×5×8×$\frac{3}{5}$=12.
点评 本题考查平面向量数量积的运算,突出考查正弦定理与余弦定理的应用,考查数形结合思想与函数方程思想及综合运算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ?x>1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | B. | ?x≤1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | C. | ?x0>1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ | D. | ?x0≤1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ |
| A. | {x|-2≤x<3} | B. | {x|x≤-2} | C. | {x|x<-2} | D. | {x|x<3} |
| A. | [-1,$\frac{1}{2}$] | B. | (-∞,-1]∪[$\frac{1}{2}$,+∞) | C. | [0,$\frac{4}{3}$] | D. | (-∞,-2]∪[$\frac{4}{3}$,+∞) |
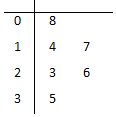 据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.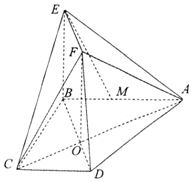 如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.
如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.