题目内容
2．已知空间直角坐标系中两点A（1，-2，3），B（-1，3，1），则|AB|=$\sqrt{33}$．分析 直接利用空间两点间距离公式求解即可．
解答 解：空间直角坐标系中两点A（1，-2，3），B（-1，3，1），则|AB|=$\sqrt{{（1+1）}^{2}+{（-2-3）}^{2}+{（3-1）}^{2}}$=$\sqrt{33}$．
故答案为：$\sqrt{33}$．
点评 本题考查空间距离公式的应用，是基础题．
练习册系列答案
相关题目
12．设变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥3x\\ x+ay≤7\end{array}\right.$，若目标函数z=x+y的最大值为14，则a值为（ ）
| A． | 1 | B． | $\frac{1}{2}$或$\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
13．函数y=${3^{\sqrt{x}}}$的值域为（ ）
| A． | （0，+∞） | B． | [1，+∞） | C． | [3，+∞） | D． | [9，+∞） |
17．定义在R上的函数y=f（x）是奇函数，且x≥0时，f（x）=ln（x2-2x+2），则x＜0时，f（x）的解析式是（ ）
| A． | f（x）=ln（-x2-2x+2） | B． | f（x）=ln（x2+2x+2） | C． | f（x）=-ln（-x2-2x+2） | D． | f（x）=-ln（x2+2x+2） |
已知圆锥的底面半径为3，母线长为5，在圆锥内部放置一个内接圆柱（圆柱的一底面与圆锥的底面重合），
14．点P（2，0）关于直线x+y+1=0对称点Q的坐标为（ ）
| A． | （-1，-3） | B． | （3，3） | C． | （-1，3） | D． | （4，-2） |
11．
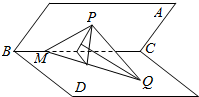如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）
如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）| A． | $\frac{2}{3}\sqrt{6}$ | B． | $\frac{3}{4}\sqrt{6}$ | C． | $\frac{4}{3}\sqrt{2}$ | D． | $\frac{3}{2}\sqrt{2}$ |
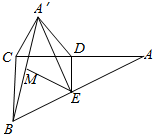已知在△ABC中，D，E分别为AC，AB的中点，沿DE将△ADE折起，使A到A′的位置，若M是A′B的中点，求证：ME∥平面A′CD．