题目内容
函数y=
|1-x|+|2x-1|的单调递减区间是 .
| 1 |
| 2 |
考点:复合函数的单调性
专题:综合题,函数的性质及应用
分析:求出t=|1-x|+|2x-1|的递增区间,即可求出函数y=
|1-x|+|2x-1|的单调递减区间.
| 1 |
| 2 |
解答:
解:令t=|1-x|+|2x-1|=
递增区间为(-∞,
),(1,+∞),
∴函数y=
|1-x|+|2x-1|的单调递减区间是(-∞,
),(1,+∞),
故答案为:(-∞,
),(1,+∞).
|
| 1 |
| 2 |
∴函数y=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(-∞,
| 1 |
| 2 |
点评:本题考查复合函数的单调性,指数函数及绝对值函数的单调性,是基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
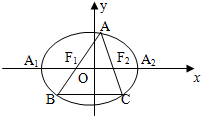 如图:A1、A2是椭圆
如图:A1、A2是椭圆