题目内容
计算：
= ．
| ||
1+
|
考点：两角和与差的正切函数,三角函数的化简求值
专题：计算题
分析：由tan60°=
，利用两角差的正切公式，即可求出答案来．
| 3 |
解答：
解：∵tan60°=
，
∴
=
=tan（60°-15°）
=tan45°
=1．
故答案为：1．
| 3 |
∴
| ||
1+
|
| tan60°-tan15° |
| 1+tan60°tan15° |
=tan（60°-15°）
=tan45°
=1．
故答案为：1．
点评：本题考查了两角差的正切公式的应用问题，解题时应熟记三角函数的恒等变换公式，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知A是△BCD所在平面外一点，M是平面ABC上的一点，试过D、M两点作一平面，使这个平面平行于BC，并说明理由．
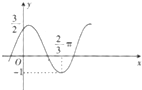将函数y=Asinωx+b（A，ω，b均为正实数）的图象向左平移| π |
| 12 |
A、y=2sin（x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
点（-5，1）关于直线x-2y+2=0的对称点是（ ）
| A、（3，3） |
| B、（-3，-3） |
| C、（5，1） |
| D、（5，-1） |
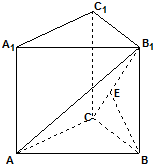如图，在直三棱柱A1B1C1-ABC中，侧面ABB1A1是边长为2的正方形，直角三角形边满足AC=BC，E是CB1上的点，且BE⊥平面ACB1．