题目内容
奇函数f(x)在(0,+∞)上的解析式是f(x)=x(x-1),则在(-∞,0)上f(x)的函数析式是 .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据已知,观察所求解析式与已知解析式所在区间关系,再利用奇偶性求解所求解析式.
解答:
解:x∈(-∞,0)时,-x∈(0,+∞),
因为f(x)在(0,+∞)上的解析式是f(x)=x(x-1),
所以f(-x)=-x(-x-1),
因为函数f(x)是奇函数,所以f(-x)=-f(x)=-x(-x-1),
所以f(x)=x(x+1),
故答案为:f(x)=x(x+1)
因为f(x)在(0,+∞)上的解析式是f(x)=x(x-1),
所以f(-x)=-x(-x-1),
因为函数f(x)是奇函数,所以f(-x)=-f(x)=-x(-x-1),
所以f(x)=x(x+1),
故答案为:f(x)=x(x+1)
点评:本题考察利用函数性质求函数解析式,主要利用所求解析式与已知解析式所在区间是对称的来求解.

练习册系列答案
相关题目
函数y=x+
的单调减区间为( )
| 4 |
| x |
| A、(-2,0)及(0,2) |
| B、(-2,0)∪(0,2) |
| C、(0,2)及(-∞,-2) |
| D、(-2,2) |
定义在集合{x|4-x2≥0}上的奇函数f(x)在区间[0,2]上是增函数,则( )
| A、f(0)<f(-1)<f(-2) |
| B、f(-1)<f(-2)<f(0) |
| C、f(-1)<f(0)<f(-2) |
| D、f(-2)<f(-1)<f(0) |
已知a,b∈R,函数f(x)=tanx在x=-
处与直线y=ax+b+
相切,设g(x)=ex+bx2+a,若在区间[1,2]上,不等式m≤g(x)≤m2-2恒成立,则实数m( )
| π |
| 4 |
| π |
| 2 |
| A、有最小值-e |
| B、有最小值e |
| C、有最大值e |
| D、有最大值e+1 |
 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: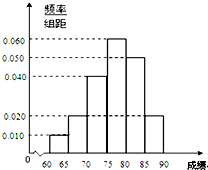 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数