题目内容
11.函数f(x)=3x-4x3(x∈[0,1])值域是( )| A. | (-∞,1] | B. | [-1,0] | C. | [0,1] | D. | [-1,1] |
分析 求导数,f′(x)=3-12x2,从而可判断出x∈[0,$\frac{1}{2}$)时,f′(x)>0,$x∈(\frac{1}{2},1]$时,f′(x)<0,这便说明$f(\frac{1}{2})$是f(x)的最大值,再比较f(0)和f(1)便可得出f(x)的最小值,从而便可得出f(x)的值域.
解答 解:f′(x)=3-12x2;
∴x∈[0,$\frac{1}{2}$)时,f′(x)>0,x∈$(\frac{1}{2},1]$时,f′(x)<0;
∴$f(\frac{1}{2})=1$为f(x)的最大值;
又f(0)=0,f(1)=-1;
∴f(x)的最小值为-1;
∴f(x)的值域为[-1,1].
故选:D.
点评 考查函数值域的概念,根据导数符号求函数最值,从而得出函数在闭区间上的值域的方法.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
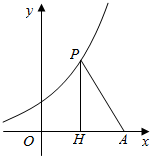 如图,已知点A(10,0),直线x=t(0<t<10)与函数y=ex+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).
如图,已知点A(10,0),直线x=t(0<t<10)与函数y=ex+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).