题目内容
已知|
|=1，
=(1，
)，(
-
)⊥
，则cos（
，
）= ．
| a |
| b |
| 3 |
| b |
| a |
| a |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：首先根据向量垂直的充要条件求出向量的数量积，进一步利用向量的坐标求出向量的模，最后利用向量的夹角公式求出结果．
解答：
解：已知(
-
)⊥
所以：(
-
)•
=0
即
•
=1
|
|=1，
=(1，
)
|
|=2
所以：cos＜
，
＞=
=
故答案为：
| b |
| a |
| a |
所以：(
| b |
| a |
| a |
即
| b |
| a |
|
| a |
| b |
| 3 |
|
| b |
所以：cos＜
| a |
| b |
| ||||
|
|
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查的知识要点：向量垂直的充要条件，向量的数量积，向量的模，向量的夹角运算．
练习册系列答案
相关题目
如图是正方体的平面展开图，则在这个正方体中：①BM与ED平行②CN与BE是异面直线
③CN与BM成60°角④DM与BN是异面直线
以上四个命题中，正确的命题序号是（ ）
| A、①②③ | B、②④ |
| C、③④ | D、②③④ |
将函数y=cos(2x-
)的图象向左平移
个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得函数图象的一条对称轴是（ ）
| π |
| 3 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
D、x=
|
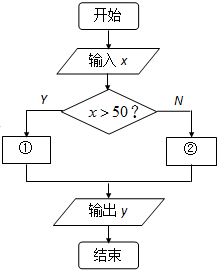某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过50kg按0.53元/kg收费，超过50kg的部分按0.85元/kg收费．相应收费系统的流程图如右图所示，则①处应填（ ）| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+（x-50）×0.85 |
| D、y=50×0.53+0.85x |
已知函数f（x）=Acos（x+φ）（A＞0，φ∈R），则“f（x）是偶函数”是“φ=π”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第202次互换座位后，小兔坐在第（ ）号座位上
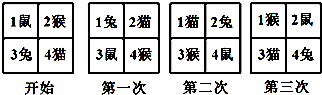
| A、1 | B、2 | C、3 | D、4 |
已知全集U={x∈N*|x＜6}，A={1，3}，B={3，5}，则∁U（A∪B）等于（ ）
| A、{1，4} |
| B、{1，5} |
| C、{2，4} |
| D、{2，5} |