题目内容
已知函数f(x)=sin(2x+
),g(x)=sin(2x-
),下列说法正确的是( )
| π |
| 3 |
| π |
| 3 |
A、f(x)的图象可以由g(x)的图象向左平移
| ||
B、f(x)的图象可以由g(x)的图象向右平移
| ||
C、f(x)的图象可以由g(x)的图象关于直线x=
| ||
D、f(x)的图象可以由g(x)的图象关于直线x=
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:函数的性质及应用,三角函数的图像与性质
分析:先求g(x+
)=f(x),故A、B不正确;求出f(x)的图象关于直线x=
对称变换而得到的函数解析式为f(2×
-x)=g(x),故C不正确,D正确;
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵g(x+
)=sin[2(x+
)-
]=sin(2x+
-
)=sin(2x+
)=f(x),
∴即由g(x)的图象向左平移
个单位得到f(x)的图象.故A、B不正确;
∵f(x)的图象关于直线x=
对称变换而得到的函数解析式为:f(2×
-x)=sin[2(
-x)+
]=sin[π-2x+
]=sin(2x-
)=g(x),故C不正确,D正确;
故选:D.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴即由g(x)的图象向左平移
| π |
| 3 |
∵f(x)的图象关于直线x=
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故选:D.
点评:本题主要考查了函数y=Asin(ωx+φ)的图象变换,直线对称变换:函数f(x)关于直线x=a对称的图象的解析式是f(2a-x)是解题的关键,属于中档题.

练习册系列答案
相关题目
已知命题p:存在x0∈R,x02-x0+1<0;命题q:“x>0,a=1”是“x+
≥2”的充分不必要条件”.则下列命题正确的是( )
| a |
| x |
| A、命题“p或q”是假命题 |
| B、命题“(¬p)且q”是真命题 |
| C、命题“p或(¬q)”是真命题 |
| D、命题“(¬p)且(¬q)”是真命题 |
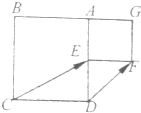 如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则
如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则