命题“若c＜0.则方程x2+x+c=0有实数解 .则( )A．该命题的逆命题为真.逆否命题也为真B．该命题的逆命题为真.逆否命题也假C．该命题的逆命题为假.逆否命题为真D．该命题的逆命题为假.逆否命题也为假题目和参考答案——青夏教育精英家教网——

题目内容

9．命题“若c＜0，则方程x²+x+c=0有实数解”，则（　　）

	A．	该命题的逆命题为真，逆否命题也为真
	B．	该命题的逆命题为真，逆否命题也假
	C．	该命题的逆命题为假，逆否命题为真
	D．	该命题的逆命题为假，逆否命题也为假

分析利用四种命题题的定义、一元二次方程的实数根与判别式的关系即可判断出．

解答解：命题“若c＜0，则方程x²+x+c=0有实数解，即原命题为真命题，
则其逆否命题也为真，
其逆命题为：方程x²+x+c=0有实数解，则c＜0，
若方程x²+x+c=0有实数解，则1-4c≥0，解得c≤$\frac{1}{4}$．故逆命题为假，
则其否命题也为假，
故选：C

点评本题考查了的逆否关系以及真假判断，是基础题，

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

18．已知等差数列{a_n}的前n项和为S_n，若S₅=8，S₁₀=20，则S₁₅等于（　　）

19．幂函数y=f（x）的图象过点$（{\sqrt{2}，\frac{1}{2}}）$，则其解析式为y=x^-2．

16．函数y=log₅x+2（x≥1）的值域是（　　）

4．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的个数是．（　　）
①若ab＞c²，则$C＜\frac{π}{3}$
②若a+b＞2c，则$C＜\frac{π}{3}$
③若a³+b³=c³，则$C＜\frac{π}{2}$
④若（a+b）c＜2ab，则$C＞\frac{π}{2}$
⑤若（a²+b²）c²＜2a²b²，则$C＞\frac{π}{3}$．

14．已知点D（x₀，y₀）为椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上一点，直线l：xx₀+yy₀=2a与直线x=±2分别交于G、H两点，且$\overrightarrow{OG}•\overrightarrow{OH}$=-2（其中O为坐标原点），则椭圆E的离心率为$\frac{\sqrt{2}}{2}$．

1．如图是棱长为1的正方体的平面展开图，则在这个正方体中，以下结论错误的是（　　）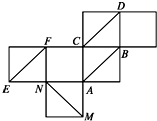

	A．	点M到AB的距离为$\frac{{\sqrt{2}}}{2}$		B．	AB与EF所成角是90°
	C．	三棱锥C-DNE的体积是$\frac{1}{6}$		D．	EF与MC是异面直线

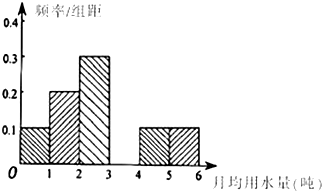为了解某市居民日常用水量的标准，某机构通过抽样获得了100位居民某年的月均用水量（单位：吨），如表是这100位居民月均用水量的频率分布表，根据如表解答下列问题：
（1）求如表中a和b的值；
（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的中位数（精确到0.01）．

分组	频数	频率
[0，1）	10	b
[1，2）	20	0.20
[2，3）	a	0.30
[3，4）	20	0.20
[4，5）	10	0.10
[5，6]	10	0.10
合计	100	1.00

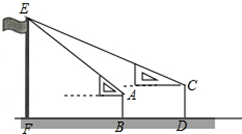某校高一年级某班开展数学活动，小李和小军合作用一副三角板测量学校的旗杆，小李站在B点测得旗杆顶端E点的仰角为45°，小军站在点D测得旗杆顶端E点的仰角为30°，已知小李和小军相距（BD）6米，小李的身高（AB）1.5米，小军的身高（CD）1.75米，求旗杆的高EF的长．（结果精确到0.1，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）