题目内容
16.函数y=log5x+2(x≥1)的值域是( )| A. | R | B. | [2,+∞) | C. | [3,+∞] | D. | (-∞,2) |
分析 由题意知y=log5x+2在x≥1为单调增函数,故函数在f(1)处取得最小值.
解答 解:由题意知:y=log5x+2在x≥1为单调增函数;
所以,f(x)min=f(1)=2;
故函数值域为:[2,+∞);
故选:B
点评 本题主要考查了对数函数的基本图形特征,利用函数单调性求函数值域,属基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
6.某四棱柱的三视图如图所示,则该四棱柱的体积为( )
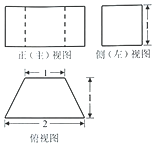

| A. | $\frac{5}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
7.已知集合A={x|x2-4<0},B={x|-1<x≤5},则A∩(∁RB)=( )
| A. | (-2,0) | B. | (-2,-1) | C. | (-2,-1] | D. | (-2,2) |
9.命题“若c<0,则方程x2+x+c=0有实数解”,则( )
| A. | 该命题的逆命题为真,逆否命题也为真 | |
| B. | 该命题的逆命题为真,逆否命题也假 | |
| C. | 该命题的逆命题为假,逆否命题为真 | |
| D. | 该命题的逆命题为假,逆否命题也为假 |
6.下列各组函数中表示同一函数的是( )
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=\left|x\right|,g(x)=\sqrt{[}3]{x^3}$ | ||
| C. | $f(x)={x^2},g(x)=\left\{\begin{array}{l}{x^2},(x>0)\\-{x^2},(x<0)\end{array}\right.$ | D. | $f(x)=\frac{{{x^2}-1}}{x-1},g(t)=t+1(t≠1)$ |
7.f(x)为偶函数,当x>0时,f(x)=2x-1,则当x<0时,f(x)=( )
| A. | 2x-1 | B. | -2x+1 | C. | 2x+1 | D. | -2x-1 |