题目内容
(本小题满分13分)已知函数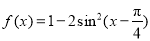 ,x∈R .
,x∈R .
(Ⅰ)求函数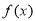 的最小正周期;
的最小正周期;
(Ⅱ)判断函数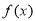 在区间
在区间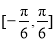 上是否为增函数?并说明理由.
上是否为增函数?并说明理由.
(Ⅰ) ; (Ⅱ)函数
; (Ⅱ)函数 在区间
在区间 上是增函数.
上是增函数.
【解析】
试题分析:(Ⅰ)因为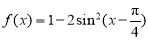 ,根据余弦的二倍角公式,可得
,根据余弦的二倍角公式,可得 ,根据三角函数的周期性,即可求出函数
,根据三角函数的周期性,即可求出函数 的最小正周期;(Ⅱ) 由
的最小正周期;(Ⅱ) 由 , 即可求出函数
, 即可求出函数 的单调递增区间为
的单调递增区间为 ,
, ,当
,当 时,知
时,知 在区间
在区间 上单调递增,即可判断函数
上单调递增,即可判断函数 在区间
在区间 上的单调性.
上的单调性.
试题解析:(Ⅰ)【解析】
因为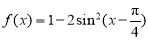
 3分
3分
 , 5分
, 5分
所以函数 的最小正周期
的最小正周期 . 7分
. 7分
(Ⅱ)【解析】
结论:函数 在区间
在区间 上是增函数. 9分
上是增函数. 9分
理由如下:
由 ,
,
解得 ,
,
所以函数 的单调递增区间为
的单调递增区间为 ,
, . 12分
. 12分
当 时,知
时,知 在区间
在区间 上单调递增,
上单调递增,
所以函数 在区间
在区间 上是增函数. 13分.
上是增函数. 13分.
考点:1.三角恒等变换;2.三角函数的性质.

练习册系列答案
相关题目
 的参数方程为
的参数方程为 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为 .(a>0.
.(a>0.  为参数),点P是圆C上的任意一点,若点P到直线
为参数),点P是圆C上的任意一点,若点P到直线 的距离的最大值为
的距离的最大值为 ,求a的值。
,求a的值。 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 ,满足对任意的
,满足对任意的 ,均有
,均有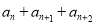 为定值.若
为定值.若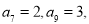
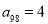 ,则数列
,则数列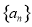 的前100项的和
的前100项的和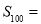 ( ).
( ).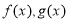 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数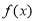 和
和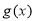 在点P处相切,称点P为这两个函数的切点. 设函数
在点P处相切,称点P为这两个函数的切点. 设函数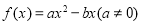 ,
,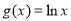 .
.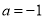 ,
,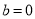 时, 判断函数
时, 判断函数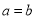 ,
,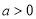 ,且函数
,且函数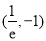 ,问是否存在符合条件的函数
,问是否存在符合条件的函数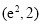 呢?(结论不要求证明)
呢?(结论不要求证明) 满足
满足 ,
, ,
, ,那么
,那么 ____.
____. ABC中,角A,B,C所对的边分别为a,b,c. 若
ABC中,角A,B,C所对的边分别为a,b,c. 若 ,
, ,则( )
,则( ) (B)
(B)
 (D)
(D)
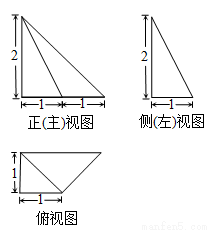
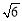
 (
( )的焦点在圆
)的焦点在圆 外,则实数
外,则实数 的取值范围是 .
的取值范围是 .