题目内容
若方程x-b=
有两个不同的实数解,则实数b的取值范围为( )
| 1-(x-2)2 |
A、[2-
| ||||
B、(2-
| ||||
C、(2-
| ||||
D、(2-
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:若方程x-b=
有两个不同的实数解,则函数y=x-b与y=
有两个交点,画出两个函数的图象,数形结合可得实数b的取值范围.
| 1-(x-2)2 |
| 1-(x-2)2 |
解答:
解:若方程x-b=
有两个不同的实数解,
则函数y=x-b与y=
有两个交点,
在同一坐标系中画出函数y=x-b与y=
的图象,如下图所示:
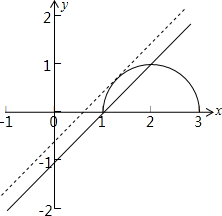
y=
的图象为以(2,0)点为圆心,以1为半径的半圆,
故当圆心(2,0)点到直线y=x-b即x-y-b=0的距离等于半径1时,直线与圆有一个交点,
此时
=1,解得:b=2-
,或b=2+
(舍),
由图可得:当b∈(2-
,1]时,函数y=x-b与y=
的图象有两个交点,
即方程x-b=
有两个不同的实数解时,实数b的取值范围为(2-
,1],
故选:B
| 1-(x-2)2 |
则函数y=x-b与y=
| 1-(x-2)2 |
在同一坐标系中画出函数y=x-b与y=
| 1-(x-2)2 |
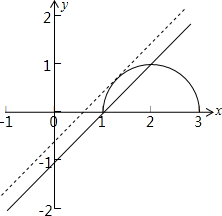
y=
| 1-(x-2)2 |
故当圆心(2,0)点到直线y=x-b即x-y-b=0的距离等于半径1时,直线与圆有一个交点,
此时
| |2-b| | ||
|
| 2 |
| 2 |
由图可得:当b∈(2-
| 2 |
| 1-(x-2)2 |
即方程x-b=
| 1-(x-2)2 |
| 2 |
故选:B
点评:本题考查方程根的个数的判断,体现了数形结合及转化的数学思想.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知复数z=-
+
i,则
=( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
命题“函数y=f(x)的导函数为f′(x)=ex+
-
(其中e为自然对数的底数,k为实数),且f(x)在R上不是单调函数”是真命题,则实数k的取值范围是( )
| k2 |
| ex |
| 1 |
| k |
A、(-∞,-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|