题目内容
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(log2a)+f(log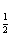 a)≤2f(1),则a的取值范围是( )
a)≤2f(1),则a的取值范围是( )
A.[1,2] B.(0,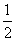 ]
]
C.[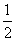 ,2] D.(0,2]
,2] D.(0,2]
C
[解析] 因为log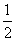 a=-log2a,所以f(log2a)+f(log
a=-log2a,所以f(log2a)+f(log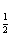 a)=f(log2a)+f(-log2a)=2f(log2a),原不等式变为2f(log2a)≤2f(1),即f(log2a)≤f(1),又因为f(x)是定义在R上的偶函数,且在[0,+∞)上递增,所以|log2a|≤1,即-1≤log2a≤1,解得
a)=f(log2a)+f(-log2a)=2f(log2a),原不等式变为2f(log2a)≤2f(1),即f(log2a)≤f(1),又因为f(x)是定义在R上的偶函数,且在[0,+∞)上递增,所以|log2a|≤1,即-1≤log2a≤1,解得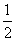 ≤a≤2,故选C.
≤a≤2,故选C.

练习册系列答案
相关题目
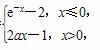 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题: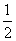 ,+∞)上恒成立,则a的取值范围是a>1;④对任意的x1<0,x2<0且x1≠x2,恒有
,+∞)上恒成立,则a的取值范围是a>1;④对任意的x1<0,x2<0且x1≠x2,恒有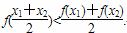
 在[-1,1]上是奇函数,则f(x)的解析式为________.
在[-1,1]上是奇函数,则f(x)的解析式为________.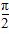 )=f(x-
)=f(x-