题目内容
3.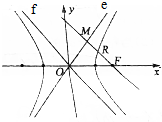 如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
分析 求得双曲线的渐近线方程,设直线FM的方程为y=-$\frac{b}{a}$(x-c),联立直线e的方程,解得M的横坐标;联立双曲线的方程可得R的横坐标,运用共线的坐标表示,解不等式结合离心率公式可得所求范围.
解答 解:设直线e的方程为y=$\frac{b}{a}$x,直线f的方程为y=-$\frac{b}{a}$x,
F(c,0),可得直线FM的方程为y=-$\frac{b}{a}$(x-c),
联立直线e的方程,解得M的横坐标为$\frac{c}{2}$,
联立双曲线的方程,可得R的横坐标为$\frac{{c}^{2}+{a}^{2}}{2c}$,
由$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],可得
$\frac{c-\frac{{c}^{2}+{a}^{2}}{2c}}{c-\frac{1}{2}c}$=1-$\frac{{a}^{2}}{{c}^{2}}$∈[$\frac{1}{2}$,$\frac{2}{3}$],
即有$\frac{1}{{e}^{2}}$∈[$\frac{1}{3}$,$\frac{1}{2}$],
即为e2∈[2,3],
解得e∈[$\sqrt{2}$,$\sqrt{3}$].
故答案为:[$\sqrt{2}$,$\sqrt{3}$].
点评 本题考查双曲线的离心率的范围,注意运用双曲线的渐近线方程,联立方程求交点,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
13.已知抛物线C:y2=4x,圆F:(x-1)2+y2=1,过点(1,0)的直线l与抛物线C及圆F交于四点,从上到下依次为A、B、C、D,若|AB|=3,则|CD|=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.已知偶函数f(x)的定义域为集合M={x|ln|x|≤5},f(5)=50,当x>0且x∈M时,xf′(x)<2f(x)恒成立,则不等式$\frac{f(x)}{{x}^{2}}$≤2的解集为( )
| A. | [-e5,-5]∪[5,e5] | B. | [-5,0)∪(0,5] | C. | [-e2,-2]∪[2,e2] | D. | [-2,0]∪(0,2] |
8.已知函数f(x)=sinωx•cosωx+$\sqrt{3}$cos2ωx-$\frac{\sqrt{3}}{2}$(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为$\frac{π}{4}$,若关于x的方程f(x)+k=0在区间[0,$\frac{π}{4}$]上有两个不同的实数解,则实数k的取值范围为( )
| A. | (-1,1) | B. | ($\frac{\sqrt{3}}{2}$,1) | C. | (-1,-$\frac{\sqrt{3}}{2}$] | D. | (-1,$\frac{\sqrt{3}}{2}$] |
13.奇函数y=f(x)在[1,2]上是增函数且有最大值5,则y=f(x)在[-2,1]上是( )
| A. | 增函数且有最小值-5 | B. | 增函数且有最大值-5 | ||
| C. | 减函数且有最小值-5 | D. | 减函数且有最大值-5 |