题目内容
18.已知偶函数f(x)的定义域为集合M={x|ln|x|≤5},f(5)=50,当x>0且x∈M时,xf′(x)<2f(x)恒成立,则不等式$\frac{f(x)}{{x}^{2}}$≤2的解集为( )| A. | [-e5,-5]∪[5,e5] | B. | [-5,0)∪(0,5] | C. | [-e2,-2]∪[2,e2] | D. | [-2,0]∪(0,2] |
分析 求出集合M,令g(x)=$\frac{f(x)}{{x}^{2}}$,求出g(x)的单调性,由$\frac{f(x)}{{x}^{2}}$≤2=$\frac{f(5)}{{5}^{2}}$,得|x|>5,结合x∈M,求出不等式的解集即可.
解答 解:由xf′(x)<2f(x),得:xf′(x)-2f(x)<0,
由ln|x|≤5,解得:-e5≤x≤e5,
令g(x)=$\frac{f(x)}{{x}^{2}}$,故g(x)的定义域是[-e5,0)∪(0,e5],
则g′(x)=$\frac{f′(x{)x}^{2}-2xf(x)}{{x}^{4}}$=$\frac{xf′(x)-2f(x)}{{x}^{3}}$<0,
∴x>0时,g(x)在定义域递减,又f(x)是偶函数,
∴x<0时,f(x)在定义域递增,
∴由$\frac{f(x)}{{x}^{2}}$≤2=$\frac{f(5)}{{5}^{2}}$,得:|x|>5,解得:x>5或x<-5,
∴不等式的解集是:[-e5,-5]∪[5,e5],
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
8.已知等差数列{an}的前15项之和为$\frac{15π}{4}$,则tan(a7+a8+a9)=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
9.P为双曲线x2-$\frac{{y}^{2}}{3}$=1的渐近线位于第一象限上的一点,若点P到该双曲线左焦点的距离为2$\sqrt{3}$,则点P到其右焦点的距离为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
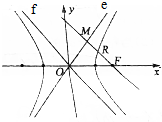 如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].