题目内容
13.奇函数y=f(x)在[1,2]上是增函数且有最大值5,则y=f(x)在[-2,1]上是( )| A. | 增函数且有最小值-5 | B. | 增函数且有最大值-5 | ||
| C. | 减函数且有最小值-5 | D. | 减函数且有最大值-5 |
分析 根据奇函数的图象关于原点对称,故它在对称区间上的单调性不变,结合题意从而得出结论.
解答 解:由于奇函数的图象关于原点对称,故它在对称区间上的单调性不变.
如果奇函数y=f(x)在[1,2]上是增函数且有最大值5,
那么f(x)在区间[-2,-1]上必是增函数且最小值为-5,
故选:A.
点评 本题主要考查函数的奇偶性和单调性的综合应用,奇函数的图象和性质,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.已知A,B为锐角三角形的两个内角,对于函数:f(x)=($\frac{sinA}{cosB}$)|x|+($\frac{sinB}{cosA}$)|x|,下列说法正确的是( )
| A. | f(x)在(-∞,0]上单调递减,在(0,+∞)上单调递增 | |
| B. | f(x)在(-∞,0]上单调递增,在(0,+∞)上单调递减 | |
| C. | f(x)在定义域上单调递增 | |
| D. | f(x)在定义域上单调递减 |
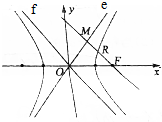 如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].