题目内容
14.若二进制数100y011和八进制数x03相等,求x+y的值.分析 直接利用进位制运算法则化简求解即可.
解答 解:100y011=1×26+y×23+1×2+1=67+8y,
x03=x×82+3=64x+3,
∴67+8y=64x+3,
∵y=0或1,x可以取1、2、3、4、5、6、7,
y=0时,x=1;y=1时,64x=72,无解;
∴x+y=1.
点评 本题考查进位制的应用,函数与方程思想的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.P为双曲线x2-$\frac{{y}^{2}}{3}$=1的渐近线位于第一象限上的一点,若点P到该双曲线左焦点的距离为2$\sqrt{3}$,则点P到其右焦点的距离为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
4.已知A,B为锐角三角形的两个内角,对于函数:f(x)=($\frac{sinA}{cosB}$)|x|+($\frac{sinB}{cosA}$)|x|,下列说法正确的是( )
| A. | f(x)在(-∞,0]上单调递减,在(0,+∞)上单调递增 | |
| B. | f(x)在(-∞,0]上单调递增,在(0,+∞)上单调递减 | |
| C. | f(x)在定义域上单调递增 | |
| D. | f(x)在定义域上单调递减 |
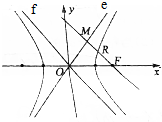 如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].