题目内容
设函数f(x)=loga(1+ax)-loga(1-ax),其中a>0,且a≠1.
(1)当a=2时,解不等式f(x)-1>0;
(2)当a>1时,若关于x的不等式f(x)-1>0恒成立,求a的取值范围;
(3)若f(x0)=x0-1,证明|x0|<1.
(1)当a=2时,解不等式f(x)-1>0;
(2)当a>1时,若关于x的不等式f(x)-1>0恒成立,求a的取值范围;
(3)若f(x0)=x0-1,证明|x0|<1.
考点:函数恒成立问题,对数函数图象与性质的综合应用
专题:函数的性质及应用,不等式的解法及应用
分析:(1)log2(1+2x)-log2(1-2x)>1,转化为:
求解即可;
(2)把不等式f(x)-1>0恒成立转化为
恒成立,进一步得到
<x<
恒成立,然后求解不等式
<
得答案;
(3)由loga(1+ax0)-loga(1-ax0)=x0-1,得到-1-
=ax0-1(ax0-1<0),分类后构造函数,由函数的单调性即可得到证明.
|
(2)把不等式f(x)-1>0恒成立转化为
|
| a-1 |
| a2+a |
| 1 |
| a |
| a-1 |
| a2+a |
| 1 |
| a |
(3)由loga(1+ax0)-loga(1-ax0)=x0-1,得到-1-
| 2 |
| ax0-1 |
解答:
(1)解:a=2时,不等式f(x)-1>0化为:log2(1+2x)-log2(1-2x)>1
即
,解得:
<x<
.
∴不等式的解集为(
,
);
(2)解:当a>1时,关于x的不等式f(x)-1>0恒成立,即loga(1+ax)-loga(1-ax)>1恒成立,
也就是
恒成立.
则
,∴
<x<
恒成立,
则
<
恒成立,解得a>0,
∴a>1;
(3)证明:由f(x0)=x0-1,得loga(1+ax0)-loga(1-ax0)=x0-1,
∴
,即-1-
=ax0-1(ax0-1<0),
当a>1时,由-
<x0<
说明|x0|<1成立;
当0<a<1时,令g(x)=-
=
,
t(x)=ax-1+1,
根据单调性可判断两函数图象交点的横坐标x0满足-1<x0<1,
故不等式|x0|<1成立.
即
|
| 1 |
| 6 |
| 1 |
| 2 |
∴不等式的解集为(
| 1 |
| 6 |
| 1 |
| 2 |
(2)解:当a>1时,关于x的不等式f(x)-1>0恒成立,即loga(1+ax)-loga(1-ax)>1恒成立,
也就是
|
则
|
| a-1 |
| a2+a |
| 1 |
| a |
则
| a-1 |
| a2+a |
| 1 |
| a |
∴a>1;
(3)证明:由f(x0)=x0-1,得loga(1+ax0)-loga(1-ax0)=x0-1,
∴
|
| 2 |
| ax0-1 |
当a>1时,由-
| 1 |
| a |
| 1 |
| a |
当0<a<1时,令g(x)=-
| 2 |
| ax-1 |
-
| ||
(x-
|
t(x)=ax-1+1,
根据单调性可判断两函数图象交点的横坐标x0满足-1<x0<1,
故不等式|x0|<1成立.
点评:本题综合考查了对数函数的性质,考查了对数不等式的解法,体现了数学转化思想方法及分类讨论的数学思想方法,属难度较大的题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目


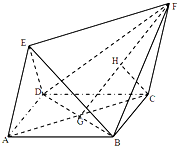 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=