题目内容
已知椭圆
+
=1上一点P,F1、F2为椭圆的焦点,若∠F1PF2=θ,求△F1PF2的面积.
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由椭圆的定义可得|PF1|+|PF2|=2a,再由余弦定理可得|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ,从而可得|PF1||PF2|=
,从而求△F1PF2的面积.
| 2b2 |
| 1+cosθ |
解答:
解:由题意,|PF1|+|PF2|=2a,
又∵|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ,
∴(|PF1|+|PF2|)2-|F1F2|2=2|PF1||PF2|+2|PF1||PF2|cosθ,
∴4a2-4c2=2|PF1||PF2|(1+cosθ),
∴|PF1||PF2|=
,
∴S△F1PF2=
|PF1||PF2|•sinθ=
sinθ.
又∵|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ,
∴(|PF1|+|PF2|)2-|F1F2|2=2|PF1||PF2|+2|PF1||PF2|cosθ,
∴4a2-4c2=2|PF1||PF2|(1+cosθ),
∴|PF1||PF2|=
| 2b2 |
| 1+cosθ |
∴S△F1PF2=
| 1 |
| 2 |
| b2 |
| 1+cosθ |
点评:本题考查了椭圆的定义及余弦定理的应用,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)在f(x)上是增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |
已知函数f(x+1)是偶函数,当x∈(-∞,1)时,函数f(x)单调递减,设a=f(-
),b=f(-1),c=f(2),a=f(-
),b=f(-1),c=f(2),则a,b,c的大小关系为 .
| 1 |
| 2 |
| 1 |
| 2 |
方程x3-x-3=0的实数解所在的区间是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
以(-4,0)、(4,0)为焦点,2a=4的双曲线的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
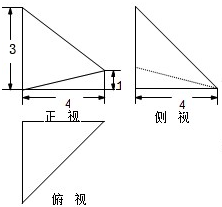 已知一个几何体的三视图如图所示,其中正视图是直角梯形.
已知一个几何体的三视图如图所示,其中正视图是直角梯形.