题目内容
11.已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时f(x)取得极值-2(I)求函数f(x)的解析式并讨论单调性
(II)证明对任意x1,x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
分析 (I)由奇函数的定义利用待定系数法求得d,再由x=1时f(x)取得极值-2.解得a,c从而确定函数,再利用导数求单调区间和极大值.
(II)由(I)知,f(x)=x3-3x(x∈[-1,1])是减函数,从而确定|f(x1)-f(x2)|最小值,证明即可.
解答 解:(I)∵f(x)为奇函数,则f(-x)=-f(x)可得d=0,
∴f(x)=ax3+cx…(2分)
f'(x)=3ax2+c,
当x=1时f(x)取得极值-2,
则$\left\{\begin{array}{l}{f′(1)=3a+c=0}\\{f(1)=a+c=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{c=-3}\end{array}\right.$,
故所求解析式为f(x)=x3-3x.
因此,f(x)=x3-3x,f'(x)=3x2-3=3(x+1)(x-1)f'(-1)=f'(1)=0
当x∈(-∞,-1)时,f'(x)>0,故f(x)在单调区间(-∞,-1)上是增函数,
当x∈(-1,1)时,f'(x)<0,故f(x)在单调区间(-1,1)上是减函数,
当x∈(1,+∞)时,f'(x)>0,故f(x)在单调区间(1,+∞)上是增函数,
∴f(x)单调递增区间(-∞,-1),(1,+∞)单调递减区间(-1,1);
(II)证明:由(1)知,f(x)=x3-3x(x∈[-1,1])是减函数,
且f(x)在[-1,1]上的最大值M=f(-1)=2,f(x)在[-1,1]上的最小值m=f(1)=-2
所以,对任意的x1,x2∈(-1,1),恒有|f(x1)-f(x2)|<M-m=2-(-2)=4,
∴不等式|f(x1)-f(x2)|<4恒成立.
点评 本小题主要考查函数的单调性及奇偶性,考查运用导数研究函数单调性及极值等基础知识,考查综合分析和解决问题的能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
| A. | [3,4) | B. | (-4,-3] | C. | (1,3] | D. | [-3,-1) |
产品A产品B(其中p、q>0)
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | 0 |
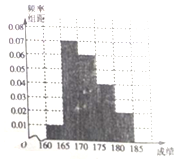 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示: