题目内容
1.已知集合M={x|-1≤x≤1},N={y|y=x2,x∈M},M∩N=( )| A. | [-1,1] | B. | [0,+∞) | C. | (0,1) | D. | [0,1] |
分析 求出N中y的范围确定出N,找出M与N的交集即可.
解答 解:∵M=[-1,1],N中y=x2,x∈M,即B=[0,1],
∴M∩N=[0,1],
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
12.已知全集U=R,集合A={x|x<-1或x>4),B={x|-2≤x≤3),那么阴影部分表示的集合为( )
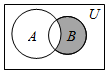

| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x≤一1} | D. | {x|-1≤x≤3} |
9.若函数f(x)=ln(x+$\sqrt{a+{x}^{2}}$)为奇函数,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | -1或1 |
16.调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
(Ⅰ)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
6.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
由此表可得回归直线方程$\widehat{y}$=-3.2x+$\widehat{a}$,据此模型预测零售价为5元时,每天的销售量为( )
| X | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 11 |
| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
10.若双曲线的顶点和焦点分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的焦点和顶点,则该双曲线方程为( )
| A. | x2-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
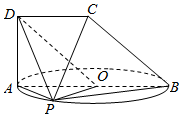 如图,梯形ABCD所在平面与以AB为直径的圆所在平面垂直,O为圆心,AB∥CD,∠BAD=90°,AB=2CD.若点P是⊙O上不同于A,B的任意一点.
如图,梯形ABCD所在平面与以AB为直径的圆所在平面垂直,O为圆心,AB∥CD,∠BAD=90°,AB=2CD.若点P是⊙O上不同于A,B的任意一点.