题目内容
13.关于x的方程x3-x2-x+m=0,至少有两个不相等的实数根,则m的最小值为$-\frac{5}{27}$.分析 利用参数分类法进行分离成m=-x3+x2+x,构造函数f(x)=-x3+x2+x,求函数的导数,研究函数极值进行求解即可.
解答 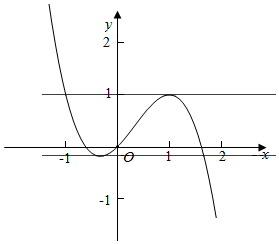 解:若方程x3-x2-x+m=0,
解:若方程x3-x2-x+m=0,
则m=-x3+x2+x,
设f(x)=-x3+x2+x,
则函数的导数f′(x)=-3x2+2x+
由f′(x)=0得x=1或x=-$\frac{1}{3}$,
由f′(x)>0得-$\frac{1}{3}$<x<1,函数f(x)单调递增,
由f′(x)><0得x<-$\frac{1}{3}$或x>1,函数f(x)单调递减,
则当x=-$\frac{1}{3}$时,函数f(x)取得极小值f(-$\frac{1}{3}$)=-(-$\frac{1}{3}$)3+(-$\frac{1}{3}$)2-$\frac{1}{3}$=$-\frac{5}{27}$,
当x=1时,函数f(x)取得极大值f(1)=-1+1+1=1,
若方程x3-x2-x+m=0,至少有两个不相等的实数根,
则$-\frac{5}{27}$≤m≤1,
故m的最小值为$-\frac{5}{27}$,
故答案为:$-\frac{5}{27}$
点评 本题主要考查函数与方程的应用,利用参数分离法,进行转化,构造函数,求函数的导数,利用导数研究函数的极值是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
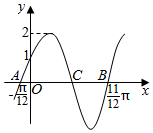
4.己知A(x1,0),B(x2,1)在函数f(x)=2sin(ωx+φ)(ω>0)的图象上,|x1-x2|的最小值$\frac{π}{4}$,则ω=( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | l | D. | $\frac{2}{3}$ |
1.已知集合M={x|-1≤x≤1},N={y|y=x2,x∈M},M∩N=( )
| A. | [-1,1] | B. | [0,+∞) | C. | (0,1) | D. | [0,1] |
8.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案有( )种.
| A. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
3.以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C的半径R取值范围是( )
| A. | (0,2) | B. | (0,$\sqrt{5}$) | C. | (0,2$\sqrt{5}$) | D. | (0,10) |