题目内容
16.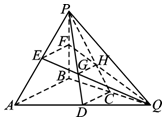 已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
分析 由题意可得GH∥EF,且GH:EF=2:3,设出三棱锥P-ABQ体积为V,可得VP-DCQ=$\frac{1}{4}V$,${V}_{P-QEF}=\frac{1}{4}V$,${V}_{P-EGHF}=\frac{5}{9}{V}_{P-EFQ}$=$\frac{5}{36}V$,作差求出多面体ADGE-BCHF的体积,则答案可求.
解答 解:∵D,C,E,F分别是AQ,BQ,AP,BP的中点,
∴EF∥AB,DC∥AB,则EF∥DC,
又EF?平面PCD,DC?平面PCD,∴EF∥平面PCD,
又EF?平面EFQ,平面EFQ∩平面PCD=GH,∴EF∥GH,
设三棱锥P-ABQ体积为V,则VP-DCQ=$\frac{1}{4}V$,${V}_{P-QEF}=\frac{1}{4}V$,
${V}_{P-EGHF}=\frac{5}{9}{V}_{P-EFQ}$=$\frac{5}{36}V$.
∴${V}_{ADGE-BCHF}=V-\frac{1}{4}V-\frac{5}{36}V$=$\frac{11}{18}V$.
∴多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
故答案为:$\frac{11}{18}$.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和思维能力,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.2${\;}^{\frac{1}{2}+lo{g}_{2}9}$的值是( )
| A. | 12$\sqrt{2}$ | B. | 9+$\sqrt{2}$ | C. | 9$\sqrt{2}$ | D. | 8+$\sqrt{2}$ |
4.函数f(x)=x2-4x+3的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
11.执行如图所示的程序框图,则输出的结果是( )
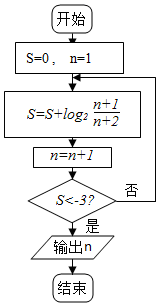

| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
6.若集合$A=({0,\left.{\frac{1}{4}}]}\right.$,则∁RA=( )
| A. | ($\frac{1}{4}$,+∞) | B. | (-∞,0]∪($\frac{1}{4}$,+∞) | C. | (-∞,0]∪[$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |
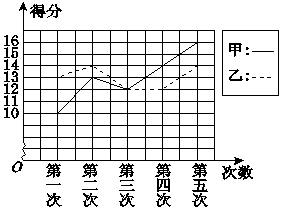 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.