题目内容
14．不等式$\frac{3}{5-3x}＞1$的解集是$（\frac{2}{3}，\frac{5}{3}）$．分析 先化简分式不等式，再等价转化为一元二次不等式，由一元二次不等式的解法求出解集．
解答 解：由$\frac{3}{5-3x}＞1$ 得，$\frac{3x-2}{5-3x}＞0$，
则（3x-2）（5-3x）＞0，即（3x-2）（3x-5）＜0，
解得$\frac{2}{3}＜x＜\frac{5}{3}$，
所以不等式的解集是$（\frac{2}{3}，\frac{5}{3}）$，
故答案为：$（\frac{2}{3}，\frac{5}{3}）$．
点评 本题考查分式不等式的解法，以及一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目
4．函数f（x）=x2-4x+3的最小值是（ ）
| A． | 3 | B． | 0 | C． | -1 | D． | -2 |
6．若集合$A=（{0，\left.{\frac{1}{4}}]}\right.$，则∁RA=（ ）
| A． | （$\frac{1}{4}$，+∞） | B． | （-∞，0]∪（$\frac{1}{4}$，+∞） | C． | （-∞，0]∪[$\frac{1}{4}$，+∞） | D． | [$\frac{1}{4}$，+∞） |
4．
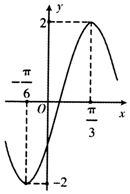函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（ ）
函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（ ）| A． | 向左平移$\frac{π}{6}$个单位长度 | B． | 向左平移$\frac{π}{12}$个单位长度 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{12}$个单位长度 |