题目内容
13. 如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.(1)求正四棱锥P-ABCD的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
分析 (1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,利用侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$,可得PO=$\sqrt{6}$,利用勾股定理建立方程,求出R;
(2)容易证明以EO$\stackrel{∥}{=}$$\frac{1}{2}PD$.可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求解
解答  解:(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,
解:(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,
∴∠PAO就是PA与底面ABCD所成的角,
∴tan∠PAO=$\frac{{\sqrt{6}}}{2}$.
又AB=2$\sqrt{2}$,则PO=AO•tan∠PAO=$\sqrt{6}$.
设F为外接球球心,连FA,
易知FA=FP,设FO=x,则
x2+4=($\sqrt{6}$-x)2,
∴x=$\frac{\sqrt{6}}{6}$,
∴正四棱锥P-ABCD的外接球半径为$\frac{5\sqrt{6}}{6}$;
(2)连结EO,由于O为BD中点,E为PD中点,所以EO$\stackrel{∥}{=}$$\frac{1}{2}PD$.
∴∠AEO就是异面直线PD与AE所成的角.
在Rt△POD中,$PD=\sqrt{O{D^2}+P{O^2}}=\frac{{\sqrt{5}}}{2}$.
∴$EO=\frac{{\sqrt{5}}}{4}$.
由AO⊥BD,AO⊥PO可知AO⊥面PBD.
所以AO⊥EO,
在Rt△OAE中,tan∠AEO=$\frac{AO}{EO}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{5}}{4}}$=$\frac{2\sqrt{10}}{5}$,
即异面直线PD与AE所成角的正切值为$\frac{{2\sqrt{10}}}{5}$.
点评 本题考查正四棱锥P-ABCD的外接球的表面积,考查学生的计算能力,正确求出正四棱锥P-ABCD的外接球的半径是关键.

| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 92 | 72 | 93 |
| 物理 | 90 | 63 | 72 | 92 | 91 | 71 | 58 | 91 | 93 | 81 | 77 | 82 | 48 | 91 | 69 | 96 | 61 | 84 | 78 | 93 |
(Ⅰ)根据上表完成下面的2×2列联表,并说明能否有99%的把握认为学生的数学成绩优秀与物理成绩优秀之间有关系?
 | 优秀 | 不优秀 | 合计 |
| 优秀 | 6 | 2 | 8 |
| 不优秀 | 2 | 10 | 12 |
| 合计 | 8 | 12 | 20 |
参考公式及数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
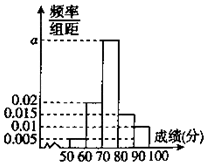 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| A. | (0,1] | B. | [-1,0) | C. | [-1,0] | D. | (-∞,1] |
| A. | y=x-3 | B. | y=-2x+1 | C. | y=2x-4 | D. | y=-2x-3 |