题目内容
18.已知幂函数$y={x}^{{p}^{2}-2p-3}$(p∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数,实数a满足$({a}^{2}-1)^{\frac{p}{3}}<(3a+3)^{\frac{p}{3}}$,则a的取值范围是(1,4).分析 根据幂函数的性质求出p的值,根据幂函数的单调性得到关于a的不等式解出即可.
解答 解:∵幂函数$y={x}^{{p}^{2}-2p-3}$(p∈N*)在(0,+∞)上是减函数,
∴p2-2p-3<0,解得-1<p<3,
∵p∈N*,
∴p=1或2.
当p=1时,y=x-4为偶函数满足条件,
当p=2时,y=x-3为奇函数不满足条件,
则不等式等价为$({a}^{2}-1)^{\frac{p}{3}}<(3a+3)^{\frac{p}{3}}$,即${{(a}^{2}-1)}^{\frac{1}{3}}$<${(3a+3)}^{\frac{1}{3}}$,
∵y=x$\frac{1}{3}$在(-∞,0)和(0,+∞)上都为增函数,
∴a2-1<3a+3<0或0<a2-1<3a+3,
解得:1<a<4,
故答案为:(1,4).
点评 本题主要考查不等式的求解,根据幂函数的性质求出幂函数的表达式是解决本题的关键.

练习册系列答案
相关题目
9.“x2-4x<0”的一个充分不必要条件为( )
| A. | 0<x<4 | B. | 0<x<2 | C. | x>0 | D. | x<4 |
13.已知椭圆的焦点F1(0,-1),F2(0,1),P为椭圆上一动点,且|F1F2|是|PF1|与|PF2|的等差中项,则椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1 | C. | x2+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
3.已知圆的方程为x2+y2-6x=0,过点(1,2)的该圆的所有弦中,最短弦的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
10.已知复数$z=\frac{1}{1+i}+i$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知a∈{0,1,2},b∈{-1,1,3,5},则函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
8.为了解市民在购买食物时看营养说明与性别的关系,现在社会上随机询问了100名市民,得到如下2×2列联表:
(1)是否有95%的把握认为:“性别与读营养说明有关系”,并说明理由;
(2)把频率当概率,若从社会上的男性市民中随机抽取3位,记这3位中读营养说明的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
参考公式和数据:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)是否有95%的把握认为:“性别与读营养说明有关系”,并说明理由;
(2)把频率当概率,若从社会上的男性市民中随机抽取3位,记这3位中读营养说明的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
| 男性 | 女性 | 总计 | |
| 读营养说明 | 40 | 20 | 60 |
| 不读营养说明 | 20 | 20 | 40 |
| 总计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
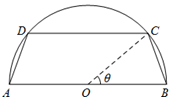 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).