题目内容
已知函数f(x)=2x-e2x+2,函数g(x)=ln(mx+1)+
,其中x≥0,m>0.
(1)求函数f(x)的单调区间;
(2)对于任意的x≥0,若恒有g(x)≥f(x)成立,求m的取值范围.
| 1-x |
| 1+x |
(1)求函数f(x)的单调区间;
(2)对于任意的x≥0,若恒有g(x)≥f(x)成立,求m的取值范围.
考点:函数单调性的性质,函数单调性的判断与证明,函数恒成立问题
专题:函数的性质及应用
分析:(1)求出函数的导函数,分析导函数在定义域上各个区间上的符号,进而可得函数f(x)的单调区间;
(2)对于任意的x≥0,若恒有g(x)≥f(x)成立,则由f(x)最大值为1可得:g(x)≥1对于任意的x≥0恒成立,分m≥2时和0<m<2时,两种情况讨论,最后综合讨论结果可得答案.
(2)对于任意的x≥0,若恒有g(x)≥f(x)成立,则由f(x)最大值为1可得:g(x)≥1对于任意的x≥0恒成立,分m≥2时和0<m<2时,两种情况讨论,最后综合讨论结果可得答案.
解答:
解:(1)∵函数f(x)=2x-e2x+2,
∴f′(x)=2-2e2x,
在(-∞,0)上,f′(x)>0,故函数的增区间为(-∞,0).
在(0,∞)上,f′(x)<0,故函数的减区间为(0,+∞).
(2)由(1)得,当x=0时,f(x)=2x-e2x+2取最大值1,
若对于任意的x≥0,恒有g(x)≥f(x)成立,
则g(x)≥1对于任意的x≥0恒成立,
∵g′(x)=
+
=
,
∵x≥0,m>0.
∴mx+1>0,
①当m≥2时,在区间(0,+∞)上,g′(x)>0,
∴g(x)的单调递增区间为(0,+∞),则当x=0时,g(x)取最小值1,满足条件;
②当0<m<2时,令g′(x)>0,解得:x>
,令g′(x)<0,解得:0<x<
,
故当x=
时,函数取最小值,此时f(
)<f(0)=1,不满足条件,
综上所述:m的取值范围为[2,+∞)
∴f′(x)=2-2e2x,
在(-∞,0)上,f′(x)>0,故函数的增区间为(-∞,0).
在(0,∞)上,f′(x)<0,故函数的减区间为(0,+∞).
(2)由(1)得,当x=0时,f(x)=2x-e2x+2取最大值1,
若对于任意的x≥0,恒有g(x)≥f(x)成立,
则g(x)≥1对于任意的x≥0恒成立,
∵g′(x)=
| m |
| mx+1 |
| -2 |
| (1+x)2 |
| mx2+m-2 |
| (mx+1)(1+x)2 |
∵x≥0,m>0.
∴mx+1>0,
①当m≥2时,在区间(0,+∞)上,g′(x)>0,
∴g(x)的单调递增区间为(0,+∞),则当x=0时,g(x)取最小值1,满足条件;
②当0<m<2时,令g′(x)>0,解得:x>
|
|
故当x=
|
|
综上所述:m的取值范围为[2,+∞)
点评:本题考查的知识点是函数单调性的性质,函数单调性的判断与证明,函数恒成立问题,是函数与导数的综合应用,难度较大.

练习册系列答案
相关题目
n(n-1)(n-2)…7等于( )
A、
| ||
B、
| ||
C、
| ||
| D、n!-7! |
程序如下:
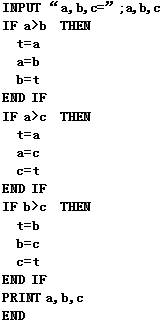
输入a=(-
)4,b=(-
)-4,c=log
,则运行结果为( )
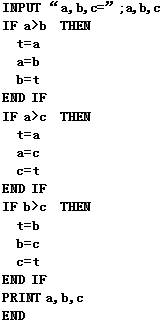
输入a=(-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|