题目内容
10.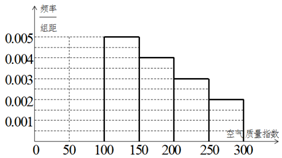 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
(Ⅱ)请在答题卡上将频率分布直方图补全(并用铅笔涂黑矩形区域),并估算这100天空气质量指数监测数据的平均数.
分析 (Ⅰ)由题意得:365b=73,a+b=0.3,由此能求出x,y,a,b的值.
(Ⅱ)补全直方图,由频率分布直方图,可估算这100天空气质量指数监测数据的平均数.
解答 解:(Ⅰ)由题意得:365b=73,解得b=0.2,
又a+b=0.3
∴a=0.1,∴x=100×0.1=10,y=100×0.2=20-------(4分)
(Ⅱ)补全直方图如图所示-------(8分)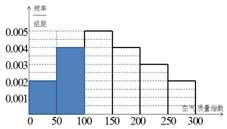
由频率分布直方图,可估算这100天空气质量指数监测数据的平均数为:
25×0.1+75×0.2+125×0.25+175×0.2+225×0.15+275×0.1=145.-------(12分)
点评 本题考查频率、频数、平均数的求法,是基础题,解题时要认真审题,注意频率分布表和频率分布直方图的性质的合理运用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
2.已知数列{an}满足an+1=$\frac{1}{{1-{a_n}}}$,若a1=$\frac{1}{2}$,则a2017=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 1 |
18.某校为了解学生学习的情况,采用分层抽样的方法从高一1000人、高二1200人、高三n人中,抽取81人进行问卷调查.已知高二被抽取的人数为30,那么n=( )
| A. | 860 | B. | 720 | C. | 1020 | D. | 1040 |
5.抛物线y2=8x的焦点为F,设A(x1,y1),B(x2,y2)是抛物线上的两个动点,若x1+x2+4=$\frac{{2\sqrt{3}}}{3}|{AB}$|,
则∠AFB的最大值为( )
则∠AFB的最大值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
14.已知数列{an},a1=1,${a_{n+1}}=\frac{{2{a_n}}}{{{a_n}+2}}$,则a10的值为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | $\frac{11}{2}$ | D. | $\frac{2}{11}$ |
1.定义在R上的偶函数f(x)满足f(2-x)=f(x),且当x∈[1,2]时,f(x)=lnx-x+1,若函数g(x)=f(x)+mx有7个零点,则实数m的取值范围为( )
| A. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | B. | $(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | ||
| C. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})$ | D. | $(\frac{1-ln2}{8},\frac{ln2-1}{6})$ |
18.下列函数中,既是偶函数,又在区间(1,2)上是减函数的为( )
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D. | y=lg$\frac{2-x}{2+x}$ |
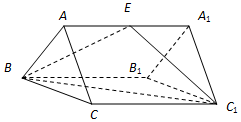 如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.
如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.